द्विघात समीकरण

परिभाषा – घात 2 वाले एक चर (जैसे x) वाले बहुपद को द्विघात समीकरण (Quadratic Equations) कहते हैं। उदाहरण – 2x² + 3x + 5, x² – 4x + 7, x² + 8, 3x² + 9x,….. आदि।

1.द्विघात समीकरण में, चर x की उच्चतम घात 2 है, इसलिए इसे द्विघाती बहुपद भी कहा जाता है।

2. किसी भी बहुपद की घात, उसके समाधानों की संख्या दर्शाती है जिन्हें शून्यक या मूल कहते हैं।

3. द्विघात समीकरण में, घात 2 है इसलिए मूल (समाधान) हमेशा दो मान होंगे।

4. किसी भी द्विघात समीकरण में, गुणांक b और c शून्य हो सकते हैं लेकिन a शून्य नहीं हो सकता क्योंकि यदि a = 0 है तो वह बहुपद द्विघाती नहीं होगा, वो रैखिक होगा।

द्विघात समीकरण(Quadratic Equations) का मानक रूप –

ax² + bx + c = 0 , जहाँ a, b, c वास्तविक संख्याएँ हैं और a ≠ 0 , x = चर (अज्ञात)

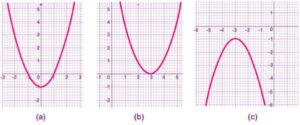
D के विभिन्न मानों के लिए ग्राफ की प्रकृति :- 

1.यदि D>0 है, तो परवलय x-अक्ष को ठीक दो अलग-अलग बिंदुओं पर काटता है। जड़ें अलग-अलग हैं। यह मामला ऊपर दिए गए चित्र में a में दिखाया गया है, जहाँ द्विघात बहुपद x-अक्ष को दो अलग-अलग बिंदुओं पर काटता है।

2. यदि D=0 है , तो परवलय x-अक्ष को केवल एक बिंदु पर स्पर्श करता है और परवलय का शेष भाग x-अक्ष के ऊपर या नीचे स्थित होता है। इस मामले में, मूल बराबर होते हैं।
यह मामला ऊपर दिए गए चित्र में b में दिखाया गया है, जहाँ द्विघात बहुपद x-अक्ष को केवल एक बिंदु पर स्पर्श करता है ।

3. यदि D<0 , तो परवलय x-अक्ष के ऊपर या नीचे पूरी तरह से स्थित होता है और x-अक्ष के साथ कोई संपर्क बिंदु नहीं होता है। इस मामले में, कोई वास्तविक मूल नहीं हैं।
यह मामला ऊपर दिए गए चित्र में c में दिखाया गया है, जहाँ द्विघात बहुपद न तो x-अक्ष को काटता है और न ही स्पर्श करता है ।

द्विघात समीकरण से संबंधित सूत्र

1.द्विघात समीकरण का मानक रूप: ax² + bx + c = 0

2. द्विघात समीकरण का विभेदक: D = b² – 4ac

3. D > 0 के लिए, मूल वास्तविक एवं भिन्न हैं।

4. D = 0 के लिए मूल वास्तविक एवं बराबर हैं।

5. D < 0 के लिए, मूल काल्पनिक हैं या मौजूद नहीं हैं।

6. द्विघात समीकरण के मूल ज्ञात करने का सूत्र: x = [-b ± √(b² – 4ac)] / 2a

7. द्विघात समीकरण के मूलों का योग: α + β = -b / a

8. द्विघात समीकरण के मूलों का गुणनफल: αβ = c / a

9. दिए गए मूलों α और β के साथ द्विघात समीकरण: x² – (α + β)x + αβ = 0