वस्तुनिष्ठ प्रश्न
1. यदि समरूप विधुत क्षेत्र Z-अक्ष के अनुरूप हो तो समविभव होगा :
(A) XY-तल
(B) XZ-तल
(C) YZ-तल
(D) कहीं भी
Answer ⇒ (A)
2. प्रत्येक r त्रिज्या तथा qआवेश से आवेशित आठ छोटे बूंदों को मिलाकर एक बड़ा बूंद बनाया जाता है तो बड़े बूंद की स्थितिज ऊर्जा प्रत्येक छोटे बूंद की तुलना में –
(A) 32 गुना होता है
(B) 16 गुना होता है ।
(C) 8 गुना होता है
(D) 4 गुना होता है।
Answer ⇒ (A)
3. एक समांतर प्लेट संधारित्र में परावैधुतांक 6 वाला परावैधुत भरना है। प्लेटों के बीच की दूरी कितनी गुनी कर देने पर धारिता पूर्ववत् बनी रहेगी ?
(A) 6 गुनी
(B) 1/6 गुनी
(C) कोई परिवर्तन नहीं
(D) इनमें से कोई नहीं
Answer ⇒ (A)
4. एक गोलीय चालक आविष्ट किया जाता है। इसके केन्द्र पर वैधुत क्षेत्र की तीव्रता होगी
(A) अनंत
(B) शून्य
(C) सतह के बराबर
(D) इनमें से कोई नहीं
Answer ⇒ (B)
5. समानान्तर प्लेट संधारित्र के प्लेटों के बीच परावैधुत पदार्थ डालने पर संधारित्र की धारिता –
(A) बढती है
(B) घटती है
(C) अपरिवर्तित रहती है
(D) कुछ कहा नहीं जा सकता
Answer ⇒ (A)
6. एक एकाकी चालक के लिए निम्न में से कौन अनुपात अचर होता है ?
(A) कुल आवेश / विभव
(B) दिया गया आवेश / विभवान्तर
(C) (कुल आवेश)2
(D) इनमें से कोई नहीं
Answer ⇒ (A)
7. वैधुत क्षेत्र में किसी द्विध्रुव को घुमाने में किया गया कार्य होता है –
(A) W = ME (1 – cos0)
(B) W = ME tan0
(C) W = ME sec0
(D) इनमें से कोई नहीं
Answer ⇒ (A)
8. यदि समरूप विधुत क्षेत्र x-अक्ष की दिशा में विद्यमान है, तो सम-विभव होगा –
(A) XY-तल की दिशा में
(B) XZ-तल की दिशा में
(Cy YZ-तल की दिशा में
(D) कहीं भी
Answer ⇒ (C)
9. 5 सेमी० त्रिज्या का एक धातु का खोखला गोला इस प्रकार आवेशित किया गया है कि इसके पृष्ठ पर विभव 10 volt गोले के केन्द्र पर विभव है –
(A) शून्य
(B) 10 volt
(C) वही जो 5 सेमी० दूर
(D) इनमें से कोई नहीं ,
Answer ⇒ (B)
10. 5μF धारिता वाले संधारित्र को 20 kV तक आवेशित करने में आवश्यक ऊर्जा का मान है –
(A) 1 kJ
(B) 10 kJ
(C) 100 kJ
(D) 5 kJ
Answer ⇒ (A)
11. यदि दो आवेशों की दूरी बढ़ा दी जाये तो आवेशों के विधुतीय स्थितिज ऊर्जा का मान –
(A) बढ़ जाएगा
(B) घट जाएगा
(C) अपरिवर्तित रहेगा
(D) बढ़ भी सकता है घट भी सकता है
Answer ⇒ (D)
12. किसी संधारित्र की धारिता व्युत्क्रमानुपाती होती है
(A) प्लेट का क्षेत्रफल
(B) प्लेटों के बीच माध्यम की परावैधुतता
(C) प्लेटों के बीच की दूरी
(D) इनमें से कोई नहीं
Answer ⇒ (B)
13. चित्र में प्लेट A पर आवेश होगा –
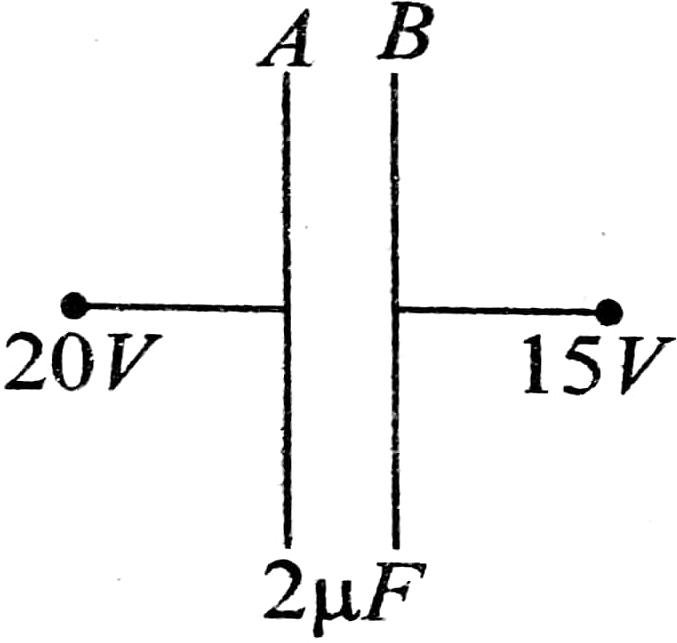
(A) -10μC
(B) 10μC
(C) zero
(D) 40μC
Answer ⇒ (B)
14. किसी विभवमापी की संवेदनशीलता को बढ़ाने के लिए –
(A) इसका अनुप्रस्थ क्षेत्रफल बढ़ाना चाहिए
(B) इसकी धारा को घटाना चाहिए
(C) इसकी धारा को बढ़ाना चाहिए
(D) इनमें से कोई नहीं
Answer ⇒ (B)
15. A तथा B के बीच समतुल्य धारिता होगी
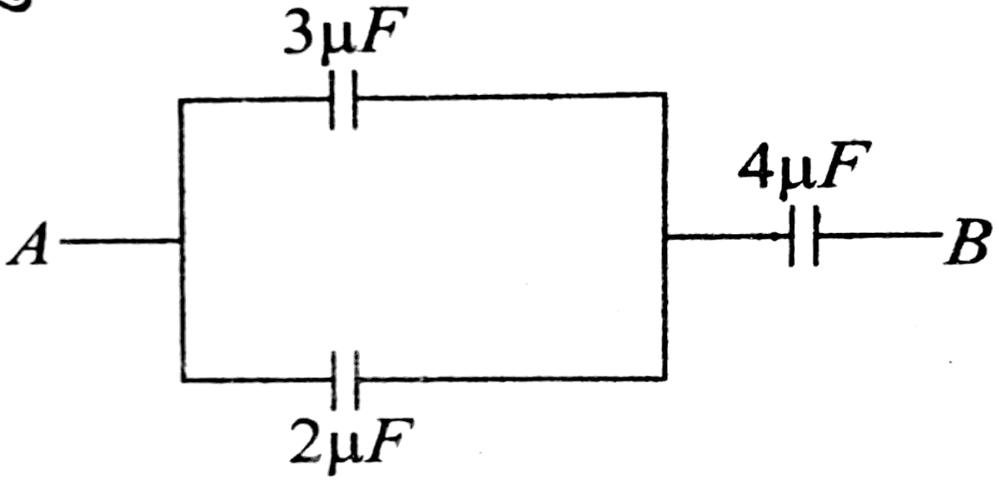
(A) μF
(B) 9μF
(C) 1μF
(D) 1/9μF
Answer ⇒ (A)
16. अलग-अलग त्रिज्याओं के दो गोलों पर समान आवेश दिये जाते हैं तो विभव होगा
(A) छोटे गोले पर ज्यादा होगा
(B) बड़े गोले पर ज्यादा होगा
(C) दोनों गोलों पर समान होगा
(D) गोलों के पदार्थ के प्रकृति पर निर्भर करता है
Answer ⇒ (A)
17. समांतर प्लेट संधारित्र के प्लेट के बीच आकर्षण बल होता है।
(A) 
(B) 
(C) 
(D) 
Answer ⇒ (B)
18. त्रिज्या 1 cm के दो चालक गोले 1m से वियुक्त हैं। दोनों पर समान आवेश 1mC दिया गया है। एक गोले का विभव v० है। अनंत पर विभव शून्य है। दूरी से सम्पर्क में लाने में किया गया कार्य –
(A) ऋणात्मक
(B) धनात्मक
(C) शून्य
(D) इनमें से कोई नहीं
Answer ⇒ (B)
19. त्रिज्या R के एक छल्ले पर धनावेश q एक समान वितरित है। अनंत पर विभव का मान शून्य लिया गया है। छल्ले की केन्द्र पर –
(A) विभव 
होगा
(B) वैधुत क्षेत्र की तीव्रता शून्य नहीं होगी
(C) विभव शून्य होगा
(D) इनमें से कोई नहीं
Answer ⇒ (A)
20. त्रिज्या R के एक छल्ले पर धनावेशq एक समान विपरीत है। अनंत पर विभव का मान शून्य लिया गया है। छल्ले की केन्द्र से दूरी पर छल्ले के अक्ष पर विभव होगा –
(A) 
(B) 
(C) 
(D) इनमें से कोई नहीं
Answer ⇒ (C)
21. त्रिज्या R के एक छल्ले पर धनावेश q एक समान वितरित है। अनंत पर विभव का मान शुन्य लिया गया है। छल्ले की केन्द्र से x-दूरी पर स्थित अक्षीय बिन्दु पर क्षेत्र की तीव्रता होगी –
(A) 
(B) 
(C) 
(D) E = 0
Answer ⇒ (A)
22. एक समविभवी तल के एक बिन्दु से दूसरे बिन्दु तक ले जाने में आवेश पर क्षेत्र द्वारा किया गया कार्य होगा –
(A) धनात्मक
(B) ऋणात्मक
(C) शून्य
(D) इनमें से कोई भी
Answer ⇒ (C)
23. विधुत् क्षेत्र में एक द्विध्रुव का आघूर्ण 
= pÎ है। इसकी स्थितिज ऊर्जा होगी –
(A) धनात्मक
(B) ऋणात्मक
(C) शून्य
(D) इनमें से कोई भी
Answer ⇒ (C)
24. X-अक्ष पर x = 0 पर q तथा x = a पर 2q आवेश रखे हैं। विभव ν का मान शून्य होगा –
(A) 0 < x < a
(B) x > a
(C) x < 0
(D) x ∞ पर
Answer ⇒ (D)
25. किसी बिन्दु P से r दूरी पर आवेश Q रखा गया है।P पर विभव V है। Pसे दुरी पर पूर्व आवेश से अलग अतिरिक्त आवेश -Q रखा जाता है।P पर विभव हो जाएगा –
(A) शून्य
(B) 2V०
(C) V०/2
(D) 3V०
Answer ⇒ (A)
26. किसी बिन्दु P से दूरी पर आवेश Q रखा गया है।P पर विभव V० है।P से r दूरी पर पूर्व आवेश से अलग अतिरिक्त आवेश Q रखा जाता है। P पर विभव होगा।
(A) शून्य
(B) 2V०
(C) V०/2
(D) 3V०
Answer ⇒ (B)
27. किसी बिन्दु P से r दूरी पर आवेश Q रखा गया है।P पर विभव v० है। P से r/2 दूरी पर एक आवेश –Q रखा जाता है। P पर विभव होगा
(A) शून्य
(B) 2V०
(C) V०/2
(D) -V०
Answer ⇒ (D)
28. दो धनावेशों (q) को एक-दूसरे से ‘a’ दूरी पर लाने में 2mJ कार्य करना पड़ता है। आवेशों q एवं -q को एक-दूसरे से दूरी पर लाने में कार्य होगा –
(A) 2 mJ
(B) -2 mJ
(C) शून्य
(D) इनमें से कोई नहीं
Answer ⇒ (B)
29. दो धनावेशों (a) को एक-दूसरे से ‘a’ दूरी पर लाने में 2mJ कार्य करना पड़ता है। तीन आवेशों q,-q एवं q को भुजा a की समबाहु त्रिभुज पर लाया गया कार्य होगा –
(A) शून्य
(B) –2mJ
(C) 4mJ
(D) अन्य
Answer ⇒ (B)
30. दो धनावेशों (q) को एक-दूसरे से ‘a’ दूरी पर लाने में 2mJ कार्य करना पड़ता है। चार आवेशों q,-q,q एवं-q को वर्ग (भुजा = a) के कोणों पर रखा गया। किया गया कार्य होगा –
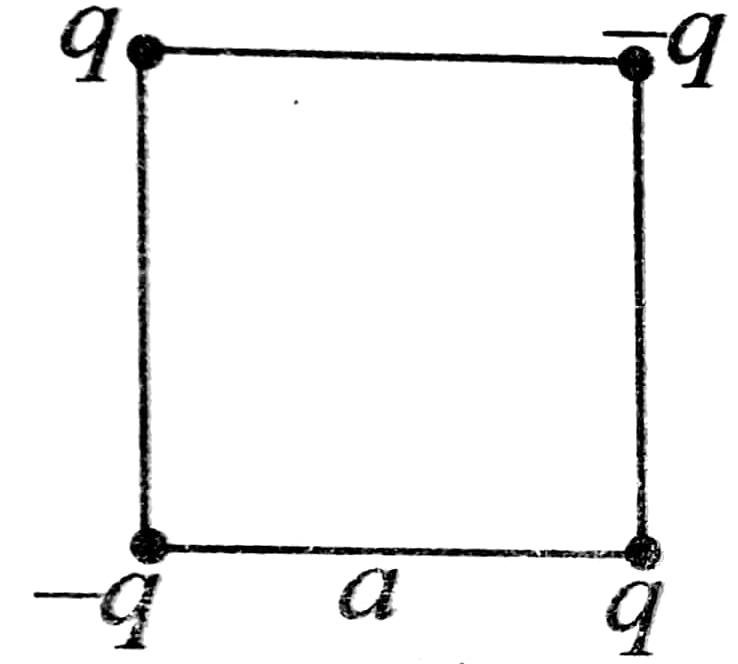
(A) 0
(B) 2mJ
(C) -2mJ
(D) इनसे भिन्न
Answer ⇒ (D)
31. एक चालक खोखले गोले के केन्द्र पर आवेश Q है। चालक पर नेट आवेश शून्य है। चालक की भीतरी सतह पर आवेश होगा
(A) शून्य
(B) Q
(C) -Q
(D) 3Q
Answer ⇒ (C)
32. एक चालक खोखले गोले के केन्द्र पर आवेश Q है। चालक पर नेट आवेश शुन्य है। चालक की बाहरी सतह पर आवेश होगा
(A) शून्य
(B) Q
(C) -Q
(D) 3Q
Answer ⇒ (B)
33. एक चालक खोखले गोले के केन्द्र पर आवेश Q है। चालक पर नेट आवेश शून्य है। चालक की केन्द्र से क्षेत्र रेखाएँ –
(A) त्रैज्य चलकर चालक पर समाप्त होंगी
(B) त्रैज्य चलेगी, चालक में शून्य होंगी एवं बाहर त्रैज्य चलेंगी
(C) त्रैज्य एवं हर जगह अशून्य होगी
(D) केवल चालक के अंदर होगी
Answer ⇒ (B)
34. त्रिज्या 1cm के दो चालक गोले 1m से वियुक्त हैं। दोनों पर समान आवेश 1mc दिया गया है। एक गोले का विभव v० है। अनंत पर विभव शून्य है। दूसरे गोले का विभव होगा –
(A) V०
(B) 2V०
(C) -V०
(D) 0
Answer ⇒ (A)
35. त्रिज्या 1cm के दो चालक गोले 1m से वियुक्त हैं। दोनों पर समान आवेश 1 mc दिया गया है। एक गोले का विभव v० है। अनंत पर विभव शून्य है। अब दोनों गोलों को सम्पर्क में लाया जाता है। सम्पर्क में स्थित गोलों के लिए –
(A) विभव v० होगा
(B) दोनों गोलों पर आवेश समान होगा
(C) आकर्षण का बल लगेगा
(D) इनमें से कोई नहीं
Answer ⇒ (B)
36. यदि एक प्रोटॉन को एक दूसरे प्रोटॉन के नजदीक लाया जाता है तो उसकी स्थितिज ऊर्जा-
(A) बढ़ेगी
(B) घटेगी
(C) अपरिवर्तित रहेगी
(D) इनमें से कोई नहीं
Answer ⇒ (A)
37. यदि 1000 बूंदें (समान आकार) एवं जिनमें प्रत्येक की धारिता 5μF, मिलकर एक बड़ी बूंद बनाती है तो बड़ी बूंद की धारिता होगी –
(A) 50 μF
(B) 100 μF
(C) 20 μF
(D) इनमें से कोई नहीं
Answer ⇒ (A)
38. दिए गए चित्र में प्लेट x पर आवेश है
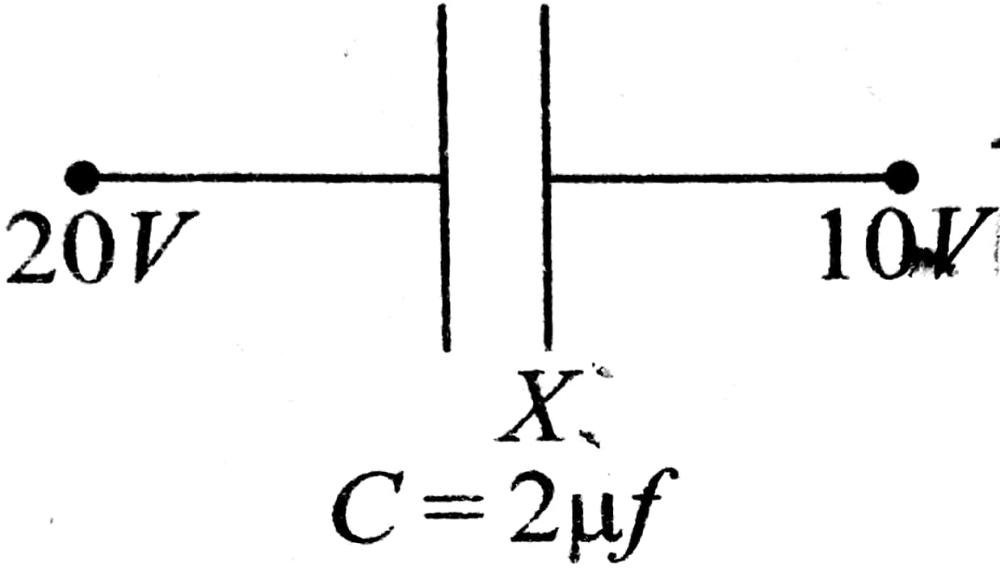
(A) -20 μC
(B) -20 μC
(C) Zero
(D) -10 μC
Answer ⇒ (B)
39. A तथा B बिन्दुओं के बीच समतुल्य धारिता है
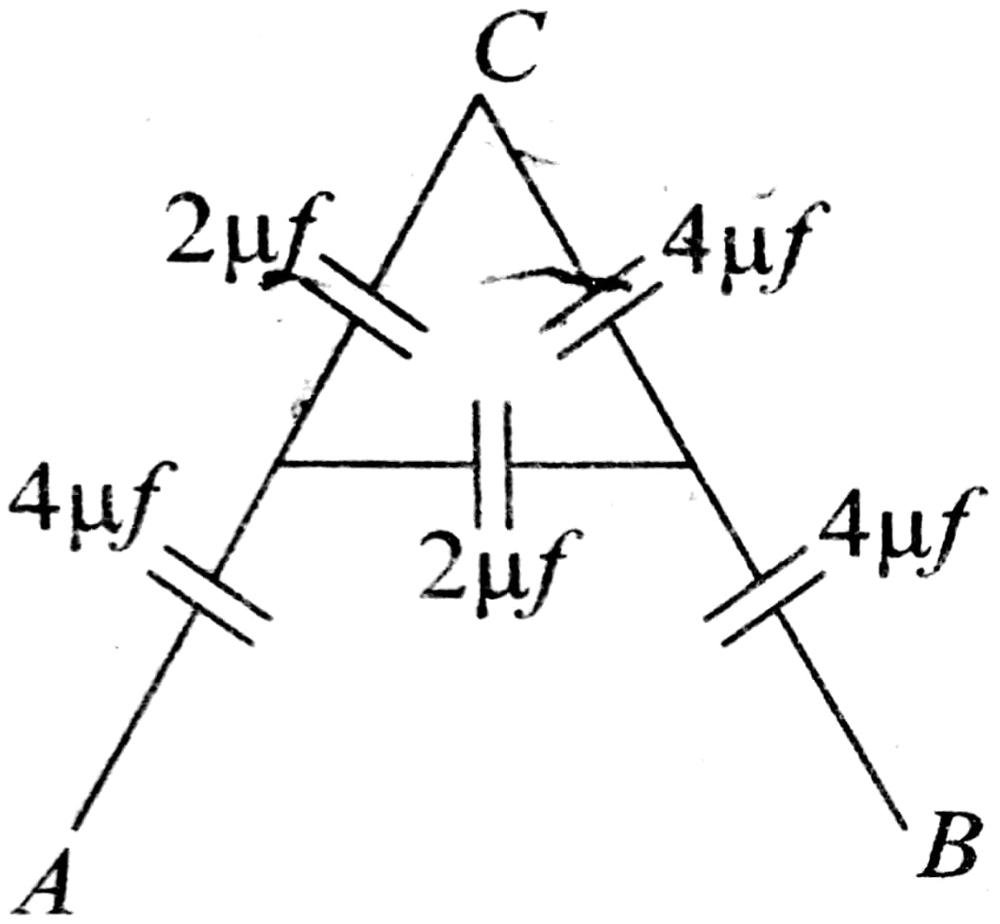
(A) 4 μF
(B) 5/4 μF
(C) 3 μF
(D) 2/3 μF
Answer ⇒ (B)
40. 64 समरूप बूंदें जिनमें प्रत्येक की धारिता 5 μF है मिलकर एक बड़ी बूंद बनाती हैं। बड़े बूंद की धारिता क्या होगी ?
(A) 4 μF
(B) 25 μF
(C) 20 μF
(D) 164 μF
Answer ⇒ (C)
41. विधुत क्षेत्र 
से लम्बवत रखे विधुत द्विध्रुव का आघूर्ण है। इस स्थिति में द्विध्रुव की स्थैतिक ऊर्जा शून्य मान लेने पर और के बीच θ कोण की स्थिति में द्विध्रुव की स्थैतिज ऊर्जा होती है
(A) 
.
(B) – .
(C) x
(D) PE (1 – cosθ)
Answer ⇒ (B)
42. इलेक्ट्रॉन-वोल्ट (eV) द्वारा मापा जाता है
(A) आवेश
(B) विभवांतर
(C) धारा
(D) ऊर्जा
Answer ⇒ (D)
43. 2 कलम्ब आवेश को एक बिंदु से दूसरे बिंदु तक ले जाने में 20 जूल कार्य की आवश्यकता होती है। इन दोनों बिन्दुओं के बीच वोल्ट में विभवान्तर है –
(A) 10
(B) 20
(C) 5
(D) 2
Answer ⇒ (A)
44. विधुत्-क्षेत्र E और विभव v के बीच सम्बन्ध होता है –
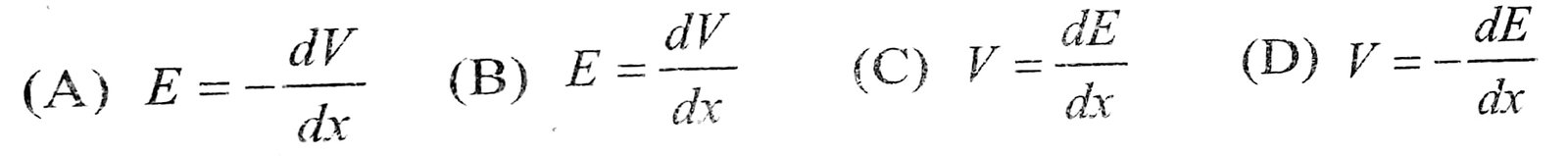
Answer ⇒ (A)
45. यदि किसी खोखले गोलीय चालक को धन आवेशित किया जाए, तो उसके भीतर का विभव –
(A) शून्य होगा
(B) धनात्मक और समरूप होगा
(C) धनात्मक और असमरूप होगा
(D) ऋणात्मक और समरूप होगा।
Answer ⇒ (B)
46. एक बिन्दु आवेश Q से r दूरी पर विधुत्-विभव का मान होता है –
Answer ⇒ (B)
47. विधुतीय विभव की विमा है –
(A) [ML2T-3 A-1]
(B) [MLT-3 A-1]
(C) [MLT-3 A-2]
(D) [ML2T-3 A-2]
Answer ⇒ (A)
48. विधुतीय आघूर्ण वाला द्विध्रुव विधुतीय क्षेत्र 
में स्थापित किया जाय, तब इसकी स्थितिज ऊर्जा होगी –
(A) x
(B) – .
(C) pE
(D) शून्य
Answer ⇒ (B)
49. तीन संधारित्र जिनमें प्रत्येक की धारिता C है श्रेणी क्रम में जोड़े गए हैं परिणामी धारिता का मान होगा –
(A) 3C
(B) 3/C
(C) C/3
(D) 1/3C
Answer ⇒ (C)
50. आवेशों5 x 10-8 C तथा -3 x 10-8 C के बीच दूरी 16 cm है। इन्हें जोड़नेवाली रेखा पर धनावेश से कितनी दूरी पर विभव शून्य होगा ?
(A) 10 cm तथा 40cm ऋणावेश की ओर
(B) 10 cm ऋणावेश की ओर
(C) 30 cm, 10 cm धनावेश की ओर
(D) इनमें से कोई नहीं
Answer ⇒ (A)
51. चित्र में प्रदर्शित परिपथ में A एवं B बिन्दुओं के बीच विभवांतर है
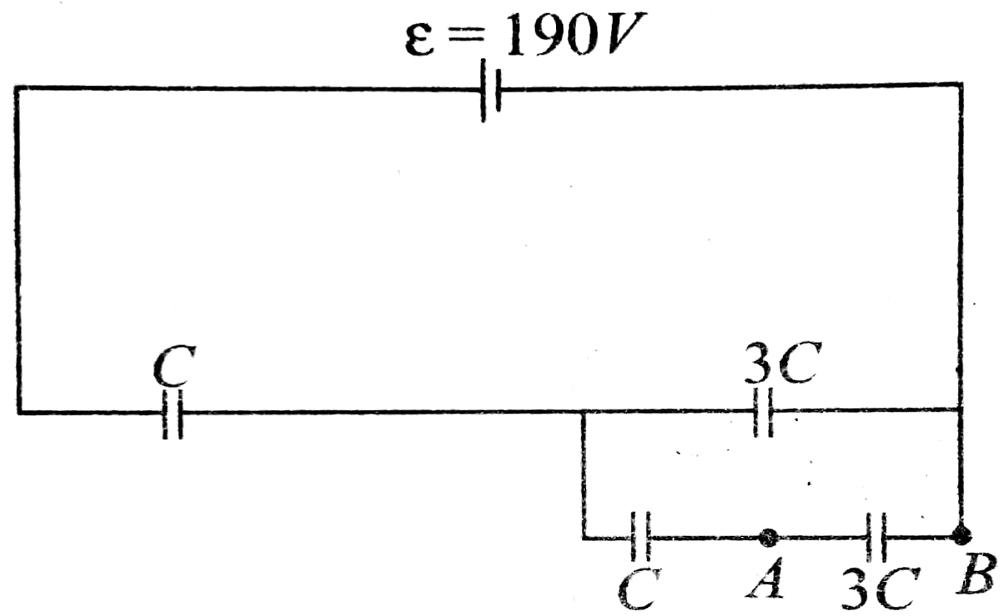
(A) 60 V
(B) 30 V
(C) 90 V
(D) 10 V
Answer ⇒ (D)
52. एक वियुक्त (isolated) गोले की धारिता n गुना बढ़ जाती है जब इसे एक भूधृत संकेन्द्रीय गोले से घेर दिया जाता है। उन गोलों की त्रिज्याओं का अनुपात होगा
(A) n / n- 1
(B) 2n / n + 1
(C) n2 + 1 / n + 1
(D) n2 / n – 1
Answer ⇒ (A)
53. प्रत्येक r त्रिज्या तथा q आवेश से आवेशित पारे की आठ बूंदें मिलाकर एक बड़ा बूंद बनाते हैं तो बड़े बूंद की धारिता प्रत्येक छोटे बूँद की धारिताओं के –
(A) 8 गुना होगा
(B) 2 गुना होगा
(C) 1/2 गुना होगा
(D) 4 गुना होगा
Answer ⇒ (B)
54. यदि इलेक्ट्रॉन का द्रव्यमान m तथा उस पर आवेश e लिया जाय और यदि यह विरामावस्था से V वोल्ट विभवांतर होकर गुजरे तो इसकी ऊर्जा होगी –
(A) me V जूल
(B) eV / m जूल
(C) eV जूल
(D) इनमें से कोई नहीं
Answer ⇒ (C)
55. यदि दो सुचालक गोले अलग-अलग आवेशित करने के बाद परस्पर जोर जायें तो –
(A) दोनों गोलों की ऊर्जा संरक्षित रहेगी
(B) दोनों का आवेश संरक्षित रहता है।
(C) ऊर्जा एवं आवेश दोनों संरक्षित रहेंगे
(D) इनमें से कोई नहीं
Answer ⇒ (B)
56. किसी द्विध्रुव को एक समरूप विधुतीय क्षेत्र में रखा गया तो उस पर परिणामी विधुतीय बल होगा –
(A) हमेशा शून्य
(B) कभी शून्य नहीं
(C) द्विध्रुव की क्षमता पर निर्भर करता
(D) इनमें से कोई नहीं
Answer ⇒ (A)
57. चित्रानुसार प्लेट 2μF संधारित्र पर आवेश होगा –
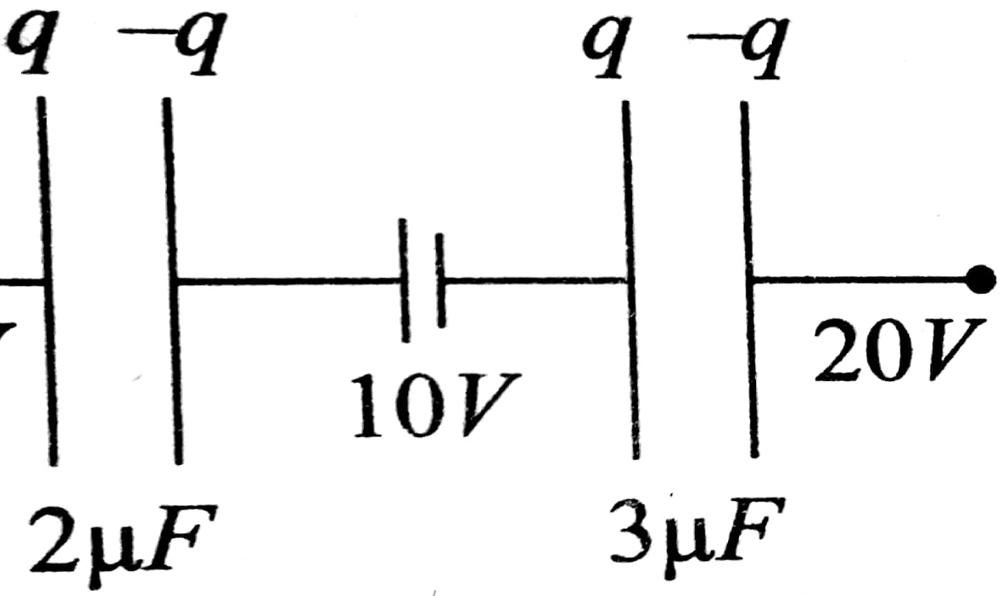
(A) 36μC
(B) 3μC से अधिक
(C) 3μC से कम
(D) शून्य
Answer ⇒ (A)
58. चन्द्रमा की धारिता लगभग होती है
(A) 177μF
(B) 711μF
(C) 1422μF
(D) इनमें से कोई नहीं
Answer ⇒ (A)
59. किसी चालक की विधुत् धारिता का व्यंजक है –
(A) C = Q / V
(B) C = V / Q
(C) C = QV
(D) C = Q2 /V
Answer ⇒ (A)
60. किसी संधारित्र की धारिता का मात्रक होता है –
(A) वोल्ट (V)
(B) न्यूटन (N)
(C) फैराड (F)
(D) ऐम्पियर (A)
Answer ⇒ (C)
61. विधुत् धारिता की विमा है
(A) [M-1L-2T4 A-2]
(B) [ML2T4 A-2]
(C) [M2L-2T4A-2]
(D) [M2L2T2A-2]
Answer ⇒ (A)
62. वायु में गोलीय चालक की धारिता समानुपाती होती है –
(A) गोले के द्रव्यमान के
(B) गोले की त्रिज्या के
(C) गोले के आयतन के
(D) गोले के सतह के क्षेत्रफल के
Answer ⇒ (B)
63. किसी संधारित्र पर आवेश की स्थितिज ऊर्जा का व्यंजक है –
(A) E = 1 / 2 CV2
(B) E = 1 / 2 QV2
(C) F = CV
(D) F = C2V2
Answer ⇒ (A)
64. दो चालकों के बीच आवेश वितरण से
(A) ऊर्जा का ह्रास होता है
(B) ऊर्जा की वृद्धि होती है,
(C) ऊर्जा का मान नियत रहता है
(D) इनमें से कोई नहीं
Answer ⇒ (A)
65. जब समांतर पट्टिका वायु संधारित्र की पट्टिकाओं के बीच की दूरी बढ़ती जाती है तब इसकी धारिता –
(A) बढ़ती जाती है
(B) घटती है
(C) में कोई परिवर्तन नहीं होता
(D) शून्य हो जाता है
Answer ⇒ (B)
66. यदि एक शीशे की छड़ (अर्थात् उच्च परावैधुत नियतांक की एक माध्यम) को हवा-संधारित्र के बीच रखा जाए तो इसकी धारिता –
(A) बढ़ेगी
(B) घटेगी
(C) स्थिर रहेगी
(D) शून्य होगी
Answer ⇒ (A)
67. संधारित्रों के श्रेणीक्रम संयोजन में जो राशि प्रत्येक संधारित्र के लिए समान रहती है, वह है –
(A) आवेश
(B) उर्जा
(C) विभवांतर
(D) धारिता
Answer ⇒ (A)
68. संधारित्रों के समांतर संयोजन में जो राशि प्रत्येक संधारित्र के लिए समान रहती है, वह है –
(A) आवेश
(B) ऊर्जा
(C) विभवांतर
(D) धारिता
Answer ⇒ (C)
69. समान धारिता के n संधारित्रों को पहले समानांतर क्रम और फिर श्रेणी क्रम में जोड़ा जाता है। दोनों अवस्थाओं की तुल्य धारिताओं का अनुपात है-
(A) n
(B) n3
(C) n2
(D) 1 / n2
Answer ⇒ (C)
70. तीन संधारित्र, जिनमें से प्रत्येक की धारिता C है, समानांतर क्रम में जुड़े हैं। उनकी समतुल्य धारिता होगी –
(A) 3 / C
(B) 3 C
(C) 1 / 2 C
(D) C / 3
Answer ⇒ (B)
71. समान धारिता के तीन संधारित्रों को श्रेणीक्रम में जोड़ने पर तुल्य 6μF धारिता होती है। यदि उन्हें समांतर क्रम में जोड़ा जाए तब तुल्य धारिता होगा –
(A) 18 μF
(B) 2 μF
(C) 54 μF
(D) 3 μF
Answer ⇒ (C)
72. 6 μF धारिता के तीन संधारित्रों को समांतर क्रम में जोड़ने पर तुल्य 0.5 μF धारिता होती है। यदि उन्हें समांतर क्रम में जोड़ा जाए तब तुल्य धारिता होगा –
(A) 16 μF
(B) 10 μF
(C) 0.4 μF
(D) 12 μF
Answer ⇒ (C)
73. 2 μF तथा 4 μF के दो संधारित्र श्रेणीबद्ध हैं तथा इनके चरम सिरों पर 1200 का विभवांतर आरोपित किया जाता है। 2 μF वाले संधारित्र पर विभवांतर है –
(A) 400 V
(B) 600 V
(C) 800 V
(D) 900 v
Answer ⇒ (C)
74. 50 μF धारितावाला एक संधारित्र 10V विभव तक आविष्ट किया जाता और ऊर्जा है।
(A) 2.5 x 10-3J
(B) 2.5 x 10-4J
(C) 5 x 10-2J
(D) 1.2 x 10-5J
Answer ⇒ (A)
75. 10 μFधारिता वाले संधारित्र 5 वोल्ट तक आवेशित किया जाएं, तो उस पर आवेश होगा –
(A) 50 C
(B) 50 x 10-6 C
(C) 5 x 10-6 C
(D) 2 C
Answer ⇒ (C)
76. दो संधारित्र जिनकी धारिताएँ,C1 तथा C2 हैं समांतर क्रम में जुड़े हैं। उनकी समतुल्य धारिता होगी।
(A) C1 – C2
(B) C2–C1
(C) C1 x C2 / C1 + C2
(D) C1 + C2
Answer ⇒ (D)
77. चार संधारित्रों में प्रत्येक की धारिता 2μF है। एक 8μF का संधारित्र बनाने के लिए उन्हें जोड़ना होगा –
(A) श्रेणीक्रम में
(B) समानांतर क्रम में
(C) कुछ श्रेणी में, कुछ समानांतर क्रम में
(D) इनमें से कोई नहीं
Answer ⇒ (B)
78. किसी भूयोजित चालक को विधुत्रोधित आवेशित चालक के निकट ले जाने पर बाद वाले चालक की विधुत्धारिता का मान –
(A) घटता है
(B) बढ़ता है
(C) अपरिवर्तित रहता है
(D) शून्य हो जाता है
Answer ⇒ (B)
79. किसी विधुतीय क्षेत्र में चालक को रखने पर उसके अन्दर विधुतीय क्षेत्र का मान –
(A) घट जाता है
(B) बढ़ जाता है
(C) शून्य होता है
(D) अपरिवर्तित रहता है
Answer ⇒ (C)
80. यदि E० बाह्य विधुतीय क्षेत्र तथा परावैधुत् का प्रभावी विधुतीय E हो तब परावैधुत् नियतांक का मान होगा –
(A) E / E०
(B) E.E०
(C) E० / E
(D) E + E०
Answer ⇒ (C)
81. वान डी ग्राफ जनित्र एक मशीन है, जो उत्पन्न करता है –
(A) एन०सी० शक्ति
(B) उच्च आवृत्ति की धाराएँ
(C) कई लाख वोल्ट का विभवांतर
(D) केवल अल्प धारा।
Answer ⇒ (C)
82. दो संधारित्र, जिसमें प्रत्येक की धारिता C है, श्रेणीक्रम में जुड़े हैं। उनको तुल्य धारिता है –
(A) 2C
(B) C
(C) C / 2
(D) 1 / 2C
Answer ⇒ (C)
83. यदि कई संधारित्र उपलब्ध हों, तो उनके समूहन से उच्चतम धारिता प्राप्त करने के लिए उन्हें जोड़ना चाहिए –
(A) श्रेणी क्रम में
(B) समान्तर क्रम में
(C) मिश्रित क्रम में
(D) इनमें से कोई नहीं
Answer ⇒ (B)
84. एक समानान्तर प्लेट संधारित्र की प्लेटों के बीच अभ्रक की एक पतली प्लेट रख देने पर उसकी धारिता –
(A) बढ़ती है
(B) सरती है
(C) समान रहती है
(D) इनमें से कोई नहीं
Answer ⇒ (A)
85. 1μF धारिता के दो संधारित्र समान्तर क्रम में जुड़े हैं और इनके श्रेणीक्रम 0.5μF में का एक तीसरा संधारित्र जुड़ा है तो परिणामी धारिता होगी –
(A) 16 μF
(B) 10 F
(C) 0.4 μF
(D) 12 μF
Answer ⇒ (C)
86. किसी वस्तु का परावैधुत् स्थिरांक हमेशा अधिक होता है –
(A) शून्य से
(B) 0.5 से
(C) 1 से
(D) 2 से
Answer ⇒ (C)
87. एक समान्तर प्लेट संधारित्र 2 परावैधुत् स्थिरांक के तेल में डुबा दिया जाता है तो दोनों प्लेटों के बीच विधुतीय क्षेत्र –
(A) 2 के समानुपाती बढ़ती है
(B) 1 / 2 के समानुपाती घटती है
(C) 
के समानुपाती घटती है
(D) इनमें से कोई नहीं
Answer ⇒ (B)
88. गोलीय संधारित्र की धारिता 1 μF है। यदि गोले के बीच की रिक्तियाँ 1 मिमी० है तो बाहरी गोले की त्रिज्या होगी –
(A) 0.30 मी०
(B) 3 सेमी०
(C) 6 मीटर
(D) 3 मीटर
Answer ⇒ (D)
89. जब संधारित्रों में K परावैधुत् स्थिरांक का माध्यम है, तो हवा की अपेक्षा उसकी धारिता –
(A) K गुना बढ़ती है
(B) K गुना घटती है
(C) K2 गुना बढ़ती है
(D) इनमें से कोई नहीं
Answer ⇒ (A)
90. प्रत्येक r त्रिज्या तथा q आवेश से आवेशित आठ छोटे बूंदों को मिलाकर एक बड़ा बूंद बनाया जाता है तो बड़े बूंद के विभव तथा छोटे बूंद के विभव का अनुपात है –
(A) 8:1
(B) 4:1
(C) 2:1
(D) 1:8
Answer ⇒ (B)
91. वैधुत क्षेत्र में किसी द्विध्रुव को घुमाने में किया गया कार्य होता है –
(A) W = ME (1 – cosθ)
(B) W = pE tan θ
(C) W = pE sec θ
(D) इनमें से कोई नहीं
Answer ⇒ (A)
92. यदि संधारित्र की प्लेटों के बीच धातु की एक छड़ घुसा दी जाय तो उसकी धारिता हो जाएगी –
(A) शून्य
(B) अनंत
(C) 9 x 109 F
(D) इनमें से कोई नहीं
Answer ⇒ (B)
93. एक आविष्ट चालक स्थिर वैधुत स्थिति में है। इसके भीतर के बिंदु पर –
(A) विभव शून्य होगा
(B) विभव प्रवणता शून्य होगी
(C) वैधुत क्षेत्र की तीव्रता की प्रवणता शून्य होगी
(D) A, B एवं C में से कोई दो
Answer ⇒ (B)
94. C1 = 2μF तथा C2 = 4μF के दो संधारित्रों को श्रेणीक्रम में जोड़ा जाता है और उनके सिरों के बीच 1200 वोल्ट (V) का विभवान्तर आरोपित किया जाता है । 2 μF वाले संधारित्र के सिरों के बीच का विभवान्तर होगा –
(A) 400 V
(B) 600 V
(C) 800 V
(D) 900 V
Answer ⇒ (C)
95. किसी सूक्ष्म विधुत द्विध्रुव के मध्य बिन्दु से बहुत दूर ‘r’ दूरी पर विधुत विभव समानुपाती होता है –
(A) r
(B) 1/r
(C) 1/r2
(D) 1/r3
Answer ⇒ (C)
96. प्रभावी धारिता 5μF को प्राप्त करने के लिए सिर्फ 2 μF के कम-से-कम कितने संधारित्र की आवश्यकता होगी ?
(A) 4
(B) 3
(C) 5
(D) 6
Answer ⇒ (A)
लघु उत्तरीय प्रश्न
1. किसी बिन्दु पर विद्युत विभव तथा तीव्रता में अंतर स्पष्ट करें।
Ans ⇒ किसी बिन्दु पर विद्युत विभव तथा तीव्रता में निम्नलिखित अंतर हैं –
| S.N | विभव | विधुत |
| 1. | विद्युत क्षेत्र में किसी बिन्दु पर विभव वह कार्य है जो एकांक धनावेश को अनन्तर से उस बिन्दु तक लाने में करना पड़ता है। | विद्युत क्षेत्र में किसी बिन्दु पर तीव्रता वह बल है जो उस बिन्दु पर रखे एकांक धनावेश पर लगता है। |
| 2. | यह एक अदिश राशि है। | यह एक सदिश राशि है। |
| 3. | इसका मात्रक वोल्ट है। | इसका मात्रक न्यूटन प्रति कूलम्ब है। |
| 4. | किसी बिन्दु पर विद्युत तीव्रता का आरेख समाकल विभव के बराबर होती है। अर्थात् V = -∫E dx है। | किसी बिन्दु पर ऋणात्मक विभव प्रवणता विद्युत तीव्रता के बराबर होती है। अर्थात् E = -dV/dx है। |
2. लम्बे आवेशित बेलनाकार चालक के कारण किसी बिन्दु पर विद्युतीय तीव्रता का व्यंजक प्राप्त करें।
Ans ⇒ माना कि R त्रिज्या के AB एक लम्ब तथा एक समान आवेशित बेलन है जिसके एकांक लम्बाई में +q आवेश है।
बेलन के अक्ष से r दूरी पर स्थित P एक बिन्दु है जिस पर विद्युतीय तीव्रता, E का मान ज्ञात करना है।
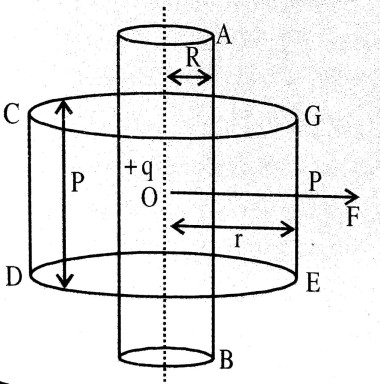
फिर माना कि 1 लम्बाई के CDEG एक बेलन है, जिसकी त्रिज्या r है जो आवेशित बेलन 4B के समाक्षीय है तथा P बिन्दु से गुजरती है।
इस बेलन की सतह अक्ष के लंबवत है।
∴ बेलन CDEG का तलीय क्षेत्रफल = 2πrl
कुल विद्युतीय फ्लक्स φ = E.2πrl
किन्तु गॉस के प्रमेय से
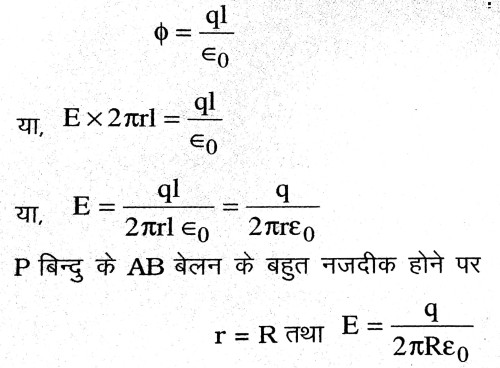
3. विद्युत फ्लक्स से आप क्या समझते हैं ?
Ans ⇒ विद्युत फ्लक्स – विद्युत क्षेत्र में स्थित किसी पृष्ठ से लम्बवत् दिशा में गुजरने वाली कुल विद्युत बल रेखाओं की संख्या को उस पृष्ठ से सम्बद्ध विद्युत फ्लक्स कहते हैं। इसे φ द्वारा व्यक्त किया जाता है।
माना कि किसी विद्युत क्षेत्र 
में किसी पृष्ठ S के छोटे से भाग का क्षेत्रफल सदिश 
विद्युत की दिशा से θ कोण बनाता है तो इस छोटे से भाग से सम्बद्ध फ्लक्स dφ = (Ecosθ)ds = 
है।
अतः सम्पूर्ण पृष्ठ से सम्बद्ध विद्युत फ्लक्स φ = ∫∫ है।
विद्युत फ्लक्स का S.I. मात्रक न्यूटन मीटर2/कूलम्ब है।
4. विद्युत विभवान्तर तथा विद्युत विभव क्या है ?
Ans ⇒ विद्युत विभवान्तर – विद्युत क्षेत्र में एकांक धनावेश को साम्य में रखते हुए, एक बिन्दु से दूसरे बिन्दु तक उसकी तीव्रता के विरुद्ध ले जाने में संपादित कार्य को उन बिन्दुओं के बीच का विभवान्तर कहते हैं। विद्युत विभवान्तर, 
होता है, जहाँ W संपादित कार्य है।
आवेश q0 मुक्त राशि पद में विद्युत क्षेत्र का वर्णन करने के लिए इसकी धारणा का प्रचलन हुआ। विभवान्तर का मात्रक वोल्ट है।
विद्युत विभव – विद्युत क्षेत्र में किसी बिन्दु पर अनन्त से एकांक धनावेश को लाने में संपादित कार्य को उस बिन्दु पर विद्युत विभव कहते हैं।
क्योंकि विद्युत क्षेत्र में किसी बिन्दु पर निरपेक्ष विभव के लिए किसी बिन्दु को निर्देश या मानक बिन्दु माना जाता है। इसको अनन्त पर माना जाता है जिसका विभव शून्य मानते हैं, क्योंकि आवेश विन्यास अनन्त पर शून्य क्षेत्र उत्पन्न करता है। अतः बिन्दु A के अनन्त होने पर B बिन्दु पर विद्युत विभव, 
है। विद्युत विभव का मात्रक भी जूल/कूलम्ब = वोल्ट होता है।
5. संधारित्र क्या है ? इसकी धारिता से आप क्या समझते हैं ?
Ans ⇒ संधारित्र – यह वैसी व्यवस्था है जिसमें विद्युत ऊर्जा को संचित किया जाता है, जिससे उसके आकार या क्षेत्रफल में परिवर्तन के बिना ही उसकी धारिता घटायी या बढ़ायी जाती है।
धारिता – “किसी चालक की धारिता आवेश का वह परिमाण है जो उसके विभव को इकाई से बढ़ा देता है।”
अथवा, “किसी चालक की धारिता, आवेश तथा विभवान्तर का अनुपात होता है।”
धारिता = आवेश/विभवान्तर
जब किसी चालक में आवेश दिया जाता है तो उसका विभव उसमें दिये गये आवेश के परिमाण के समानुपाती बढ़ जाता है।
माना कि q आवेश के परिमाण चालक को दिया गया है, जिससे उसमें V विभव बढ़ता है तो q α V
या, q = CV,
जहाँ C एक चालक का स्थिरांक है, जो आकार, रूप तथा घिरे हुए माध्यम पर निर्भर करता है तथा चालक की धारिता कहलाता है।
∴ C = q/V धारिता का मात्रक फैराड है। एक फैराड = कूलम्ब/ वोल्ट होता है। यह एक बड़ा मात्रक है। छोटे मात्रकों में माइक्रो फैराड (μF) या पिको फैराड (pF) का प्रयोग किया जाता है।
धारिता का विमासूत्र [M-1L-2T4A2] है।
6. प्रमाणित करें कि एक विलगित गोलाकार चालक की धारिता उसकी त्रिज्या के अनुक्रमानुपाती होती है।
Ans ⇒ माना कि r त्रिज्या का एक विलगित गोलाकार चालक +q आवेश से समान रूप से आवेशित है, तो उसकी सतह पर विद्युत विभव, 
है।
अतः विलगित गोलाकार चालक की धारिता,
7. परावैद्युत पदार्थ से आप क्या समझते हैं ? अथवा, संधारित्र में परावैद्युत का क्या कार्य है ?
Ans ⇒ परावैद्युत पदार्थ – वैसे पदार्थ परावैद्युत कहलाते हैं, जिन्हें संधारित्र की प्लेटों के बीच रखने पर उन प्लेटों के बीच विभवान्तर का मान कम होता है अर्थात् उसकी धारिता बढ़ जाती है । परावैद्युत पदार्थ विद्युत विरोधी होता है। जैसे-काँच, अभ्रक, पैराफिन, मोम, तेल आदि।
8. दो चालकों की धारिताएँ C1 तथा C2 है और उनके विभव क्रमश: V1 तथा V2 हैं। इन्हें आपस में किसी तार द्वारा जोड़ देने पर उनके विभव में परिवर्तन क्रमश: ΔV1 तथा ΔV2 होता है, तो प्रमाणित करें कि 
Ans ⇒ प्रमाण : दोनों चालकों को एक तार से जोड़ने पर आवेश ऊँचे विभव वाले चालक से निम्न विभव वाले चालक की तरफ दोनों चालकों पर उभयनिष्ठ विभव (एक समान विभव) होने तक प्रवाहित होता है।
9. विद्युतशीलता या परावैद्युतता तथा पराविद्युत स्थिरांक या विशिष्ट प्रेरणधारिता से आप क्या समझते हैं ?
Ans ⇒ विद्युतशीलता या परावैद्युतता तथा पराविद्युत स्थिरांक या विशिष्ट प्रेरणधारिता किसी माध्यम की विद्युतशीलता आपेक्षिक विद्युतशीलता तथा निर्वात की विद्युतशीलता का गुणनफल होता है। माना कि किसी माध्यम की विद्युतशीलता आपेक्षिक विद्युतशीलता εr तथा निर्वात की विद्युतशीलता ε0 है तो हम पाते हैं कि ε = εrε0
या, 
माध्यम या निर्वात की विद्युतशीलता का मात्रक न्यूटन मीटर2/कूलम्ब2 है। किन्तु आपेक्षिक विद्युतशीलता का कोई मात्रक नहीं होता है। आपेक्षिक विद्युतशीलता को पराविद्युत स्थिरांक भी कहते हैं। इसे K द्वारा व्यक्त किया जाता है। इसलिए पराविद्युत स्थिरांक K का भी कोई मात्रक नहीं है।
. 
वायु या निर्वात के लिए εr या K का मान 1 (एक) है। पराविद्युत स्थिरांक को विशिष्ट प्रेरण धारिता भी कहते हैं।
10. विद्युत ध्रुवण तथा विद्युत विस्थापन से आप क्या समझते है ?
Ans ⇒ विद्युत ध्रुवण – विधुत क्षेत्र में प्रति एकांक आयतन के द्विध्रुव आघूर्ण को विधुत द्विध्रुव कहते है। इसे P द्वारा व्यक्त किया जाता है।
माना कि विद्युत क्षेत्र में स्थित किसी भी पदार्थ के प्रत्येक अणु या परमाणु का द्विध्रुव आघूर्ण p है तथा प्रति एकांक आयतन में अणुओं या परमाणुओं की संख्या n है, तो माध्यम का ध्रुवण, P = np होता है।
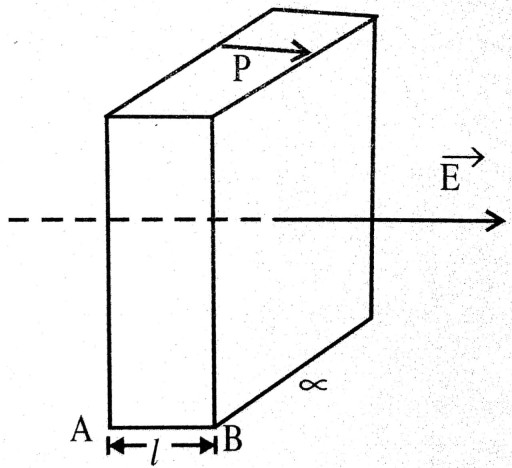
ध्रुवण का S.I मात्रक कूलम्ब/मीटर² है।
माना कि किसी विद्युत क्षेत्र के लम्बवत् स्थित 1 मुटाई एवं α अनुप्रस्थ काट की एक पराविद्युत सिल्ली AB का ध्रुवण क्षेत्र की दिशा के अनुरेखा P है, तो सिल्ली का कुल विद्युत द्विध्रुव आघूर्ण, p = P (1∝) = (Pα)1 है। चूँकि सिल्ली की सतह A तथा B के बराबर एवं विपरीत आवेश एक-दूसरे से 1 दूरी पर स्थित होने के कारण ध्रुवित आवेश = Pα तथा उसका तलीय घनत्व, σp = P होता है।
विद्युत विस्थापन – जब आविष्ट चालक के सम्पर्क में किसी विद्युत माध्यम को लाया जाता है तो माध्य के ध्रुवण के कारण चालक का प्रभावी आवेश एवं विद्युत क्षेत्र कम हो जाता है । माना कि चालक के मुक्त आवेश का तलीय घनत्व σ तथा इसके सम्पर्क में स्थित माध्यम के पृष्ठ पर ध्रुवण के फलस्वरूप उत्पन्न विपरीत आवेश का तलीय घनत्व -σp है, तो चालक का प्रभावी तलीय घनत्व σ’= σ-σp है।
अतः कूलम्ब प्रमेय से पराविद्युत माध्यम में स्थित चालक के समीप विद्युत क्षेत्र की तीव्रता
जहाँ 
द्वारा परिभाषित राशि को विद्युत विस्थापन कहते हैं। पराविद्युत माध्यम में स्थित चालक की सतह के किसी बिन्दु से अभिलम्बवत् विद्युत विस्थापन का घटक चालक के मुक्त आवेश के तलीय घनत्व के बराबर है।
अतः किसी भी बंद पृष्ठ पर विद्युत विस्थापन का फ्लक्स उस पृष्ठ के अन्दर स्थित मुक्त आवेश के बराबर होता है।
अर्थात् 
जहाँ, ds चालक का अल्पांश पृष्ठ, 
एकांक सदिश तथा 
है।
11. (a) क्या r दूरी पर Q1 और Q2 आवेश से आवेशित दो बड़े गोले पर स्थिर वैद्युत बल का परिमाण निश्चित रूप से Q1Q2/4πε0r² द्वारा दर्शाया जाता है ?
(b) यदि कूलॉम के नियम में निर्भरता में 1/r³ हो तो क्या गाउस का नियम सत्य होगा ?
(c) स्थिर वैद्युत क्षेत्र विन्यास में एक छोटा परीक्षण आवेश किसी बिन्दु पर विराम में छोड़ा जाता है। क्या यह उस बिन्दु से होकर जाने वाली क्षेत्र रेखा के अनुदिश चलेगा?
(d) इलेक्ट्रॉन की पूर्ण वृत्तीय कक्षा में नाभिक के क्षेत्र द्वारा कितना कार्य किया जाता है ? यदि कक्षा दीर्घ वृत्ताकार हो तो क्या होगा ?
(e) आवेशित चालक के पृष्ठ पर वैद्युत क्षेत्र असतत होता है। क्या वहाँ वैद्युत विभव की असतत होगा ?
(f) किसी एकल चालक की धारिता से आपका क्या अभिप्राय है ?
(g) एक संभावित उत्तर की कल्पना कीजिए कि पानी का परावैद्युतांक (= 80) अभ्रक के परावैद्युतांक (= 6) से अधिक क्यों होता है ?
Ans ⇒ (a) स्थिर वैद्युत बल का परिमाण निश्चित रूप से Q1Q2/4πε0r² नहीं होगा क्योंकि गोले का आवेश का वितरण समान नहीं है।
(b) कूलॉम के नियम में निर्भरता 1/r³ हो तो गाउस का नियम सत्य नहीं होगा।
(c) जब क्षेत्र रेखा सरल रेखा हो तब परीक्षण आवेश क्षेत्र के अनुदिश चलेगा अन्यथा यह आवश्यक नहीं है।
(d) किया गया कार्य शून्य होगा तथा कक्षा की आकृति पर निर्भर नहीं करता है।
(e) आवेशित चालक के पृष्ठ पर वैद्युत विभव सतत होगा।
(f) एकल चालक पर संघारित्र है जिसका दूसरा प्लेट अनंत पर है।
(g) पानी के अणु ध्रुवीय होते हैं जबकि अभ्रक के अध्रुवीय, पानी के अणुओं में स्थायी द्विध्रुव आघूर्ण है। अतः पानी का परावैद्युतांक अभ्रक आदि के परावैद्युतांक से कहीं अधिक होता है।
12. निम्नलिखित में संगत समविभवी पृष्ठ को लिखें
(a) Z-दिशा में अचर वैद्युत क्षेत्र
(b) एक क्षेत्र जो समान रूप से बढ़ता है परन्तु एक ही दिशा (मान लीजिए Z-दिशा) में रहता है।
(c) मूल बिन्दु पर कोई एकल धनावेश और
(d) एक समतल में समान दूरी पर समांतर लम्बे आवेशित तारों से बने एकसमान जाल।
Ans ⇒ (a) X-Y तल के समांतर पृष्ठ ।
(b) समविभवी तल X-Y तल के समांतर होता है किन्तु ये एक-दूसरे के समीप होते हैं जब क्षेत्र बढ़ता है।
(c) सकेन्द्री गोले का केन्द्र मूल बिन्दु पर।
(d) ग्रीड के अतिसमीप विद्युत क्षेत्र असमान होने से समविभवी सतह बदलते हुए आकृति का होता है। ग्रीड से बहुत दूर विद्युत क्षेत्र समरूप और तल के समान्तर होता है। अतः समविभवी तल ग्रीड के तल के समांतर होती है।
13. त्रिज्या तथा q1 आवेश वाला एक छोटा गोला, r2 त्रिज्या और आवेश के गोलीय खोल (कोश) से घिरा है। दर्शाइए यदि q1 धनात्मक है तो (जब दोनों को एक तार द्वारा जोड़ दिया जाता है) आवश्यक रूप से आवेश, गोले से खोल की तरफ ही प्रवाहित होगा, चाहे खोल पर आवेश q2 कुछ भी हो।
Ans ⇒ यहाँ r2, r1 छोटे गोल और गोलीय खोल की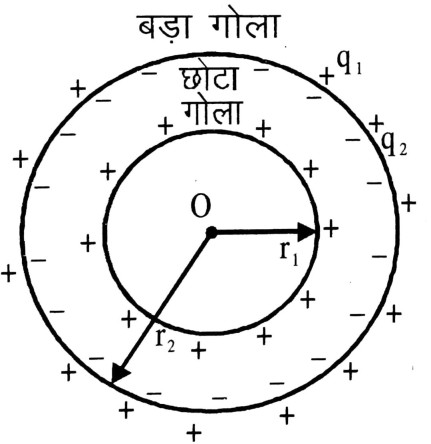 
क्रमशः त्रिज्याएँ हैं। खोल गोल को घेरे हुए हैं। +q1 आवेश गोल पर है तथा +q2 आवेश खोल पर। हमें ज्ञात है कि आवेशित चालक के भीतर विद्युत क्षेत्र शून्य होता है अर्थात् E = 0, इस प्रकार गाउस के सिद्धांत से
(गोलीय खोल में q2 = 0 क्योंकि E = 0 इसके अन्दर)
यहाँ q2 खोल के बाहरी पृष्ठ पर होना चाहिए। अब + q1 आवेश वाला गोल खोल अन्दर बन्द है। अतः खोल के आन्तरिक पृष्ठ पर -q1 आवेश और बाहरी पृष्ठ पर +q1 आवेश उत्प्रेरित होंगे।
∴ खोल के बाहरी पृष्ठ पर कुल आवेश q2 + q1
आवेश सदैव बाहरी पृष्ठ पर रहता है। इसलिए q1 आवेश गोल के बाहरी पृष्ठ से खोल के बाहरी पृष्ठ की ओर उस सम प्रवाहित होगा जब उन्हें तार से जोड़ते हैं।
14. (a) पृथ्वी के सतह के समीप विद्युत तीव्रता 100 vm-1 है। जब हम घर से बाहर जाते हैं तो हमें विद्युत आघात क्यों लगता है ?
(b) एक व्यक्ति शाम के समय अपने घर से बाहर 2m ऊँचा अवरोधी पट्ट रखता है जिसके शिखर पर एक 1m2 क्षेत्रफल की बड़ी एल्युमिनियम की चादर है। अगली सुबह वह यदि धातु की चादर को छूता है तो क्या उसे विद्युत आघात लगेगा ?
(c) वायु की चालकता के कारण सारे संसार में औसतन वायुमंडल में विसर्जन धारा 1800 A है। तब यथासमय वातावरण स्वयं पूर्णतः विसर्जन द्वारा विद्युत उदासीन क्यों नहीं हो जाता है ? दूसरे शब्दों में वातावरण को कौन आवेशित करता है ?
(d) तड़ित के दौरान वातावरण की वैद्युत ऊर्जाओं के रूप क्षय होती है।
Ans ⇒ (a) हमारा शरीर और पृथ्वी समविभवी सतह बनाता है। अतः हमारे सिर और पृथ्वी के बीच विद्युत क्षेत्र नहीं होता है जिसके कारण हमें विद्युत आघात नहीं लगता है।
(b) हाँ, यदि वह धातु की पट्टी को अगली सुबह छूता है तो उसे बिजली का झटका लगेगा। इसका कारण है कि एल्युमिनियम की पट्टी और पृथ्वी एक धारित बनाती है जिसमें अवरोधी पट्टी (स्लैब) एक परावैद्युत बनाती है। आवेश की नीचे की ओर वर्षा से एल्युमिनियम की पट्टी का विभव बढ़ जाता है अर्थात् 1800 A की अनावेशित धारा द्वारा यह आवेशित हो जाती है जो वायुमंडल से नीचे आ रही है (धारा)। जब हम एल्युमिनियम की पट्टी को छूते हैं तो धारा हमारे शरीर से होकर पृथ्वी में चली जाती है। यह आवेश प्रवाह एक विद्युत धारा बनाता है और हम झटका अनुभव करेंगे।
(c) वायु की थोड़ी चालकता के कारण पूरे संसार में प्रति सेकेण्ड 1800 C आवेश पृथ्वी में पंप होता है। तड़ित और तड़ित झंडा के लगातार होते रहने से पृथ्वी में प्रति सेकेण्ड – 1800 C आवेश भेजता है। यह पृथ्वी और समतापमंडल के बीच विद्युत विभव बनाये रखता है जिससे विद्युत विसर्जन द्वारा वातावरण उदासीन नहीं होता है।
(d) तड़ित के दौरान विद्युत ऊर्जा का ऊष्मा ऊर्जा और ध्वनि ऊर्जा के रूप में क्षय होता है।
15. चित्र में ऋण आवेश की क्षेत्र रेखाएँ दर्शायी गयी है।
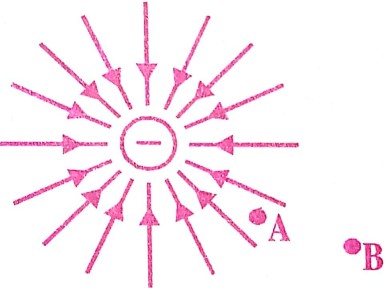(a) VB – VA के चिह्न बतावें।
(b) A और B के बीच एक छोटे से ऋण आवेश की स्थितिज ऊर्जा में अंतर का चिह्न बतावें ।
(c) B से A तक छोटे से ऋण आवेश को ले जाने के लिए बाह्य साधन द्वारा किया गया कार्य का चिह्न बतावें।
(d) B से A तक ले जाने में क्या छोटे-से ऋणावेश की गतिज ऊर्जा बढ़ेगी या घटेगी ?
Ans ⇒ (a) A और B पर विद्युत विभव –ve होता है।
∴ rB > rA
इसलिए B पर विद्युत विभव का मान A पर के विद्युत विभव से कम ऋणात्मक होगा।
∴ VB – VA > 0
(b) दोनों ऋण आवेश के कारण स्थितिज ऊर्जा धनात्मक होता है।
अतः (P.E.)A > (P.E.)B या, – (P.E.)A – (P.E.)B > 0
(c) ऋण आवेश को B से A तक लाने में विकर्षण बल के विरुद्ध किया गया कार्य धनात्मक होगा।
(d) B से A तक ऋण आवेश को लाने में स्थितिज ऊर्जा बढ़ती है। अतः B से A तक ले जोने में गतिज ऊर्जा घटेगी।
16. विद्युत क्षेत्र के किसी बिन्दु पर विभव एवं तीव्रता के बीच सम्बन्ध स्थापित करें।
Ans ⇒ माना कि O पर + qआवेश है। इस आवेश के विद्युत क्षेत्र A और B दो बिन्दु एक दूसरे के समीप Δx दूरी पर है, माना कि A और B पर विद्युत विभव क्रमशः V + ΔV और V है।
A और B के बीच विभवान्तर = V + ΔV – V = ΔV
A और B के बीच विद्युत तीव्रता E है।
एकांक धन आवेश को B से A तक लाने में किया गया कार्य ΔW = -EΔX
ऋणात्मक चिह्न का अर्थ कि विद्युत तीव्रता E की दिशा विस्थापन Δx के विपरीत है। यह किया गया कार्य ΔW विभवान्तर ΔV के बराबर होता है।
अतः विद्युत क्षेत्र में किसी बिन्दु पर विद्युत तीव्रता विभव प्रवणता के ऋणात्मक मान बराबर होता है।
17. (i) साधारण रबर विद्युतरोधी है। परंतु वायुयान के विशेष रबर के पहिए हल्के चालक बनाए जाते हैं। क्यों ?
(i) जो वाहन ज्वलनशील पदार्थ ले जाते हैं उनकी धातु की रस्सियाँ वाहन के गतिमय होते धरती को छती रहती है, क्यों ?
(iii) एक चिडिया एक उच्च शक्ति के खले बिजली के तार पर बैठी है, और उसको कछ नहीं होता। धरती पर खड़ा व्यक्ति उसी तार को छता है, तो उसे घातक धक्का लगता है, क्यों ?
Ans ⇒ (i) वायुयान के उतरते समय टायर और धरती के बीच घर्षण से बडी परिमाण में आवेश उत्पन्न होता है। टायर को हल्का चालक बनाने से आवेश टायर पर जमा नहीं होता है अपितु धरती में चला जाता है।
(ii) वाहन के गति के दरम्यान हवा के घर्षण वाहन आवेशित हो जाता है। यदि आवेश अधिक परिमाण में हो तो स्पार्क उत्पन्न हो सकता जो वाहन को जला सकता है। इसे रोकने के लिए धातु की रस्सी वाहन से धरती को । छूता रहता है जिससे वाहन पर आवेश संचित नहीं होता है।
(iii) जब चिड़ियाँ उच्च शक्ति के खुले तार पर बैठती है तब उसे कुछ नहीं होता है क्योंकि चिड़िया और पृथ्वी के बीच परिपथ पूरा नहीं होता है। यदि आदमी तार को छूता है तब पृथ्वी से इसके शरीर के द्वारा परिपथ पूरा हो जाता है और उच्च धारा शरीर से बहने लगती है जिससे जोर का धक्का लगता है।
18. समविभवी तल से क्या समझते हैं ?
Ans ⇒ विद्युत क्षेत्र में समविभवी तल एक ऐसा तल है जिसके सभी बिन्दुओं पर विद्युत विभव का मान समान होता है।
समविभवी तल में धन आवेश को एक बिन्दु से दूसरे बिन्दु तक लाने में किया गया कार्य शून्य होता है।
समविभवी तल में प्रत्येक बिन्दु पर विद्युत क्षेत्र की दिशा तल के लम्बवत् होती है।