विधुत आवेश तथा क्षेत्र

वस्तुनिष्ठ प्रश्न

1. किसी वस्तु पर आवेश की न्यूनतम मात्रा कम नहीं हो सकती है

(A) 1.6 x 10^-19 कूलम्ब से
(B) 3.2 x 10^-19 कूलम्ब से
(C) 4.8 x 10^-19 कूलम्ब से
(D) 1 कूलम्ब से

Answer ⇒ (A)

2. एक लंबे समरूप आविष्ट सीधे तार से दूरी ‘r’ पर विद्युत क्षेत्र की तीव्रता E1 एवं दूरी 2r पर विद्युत क्षेत्र की तीव्रता E2 है। E1 एवं E2 का अनुपात होगा :

(A) 1/2
(B) 2/1
(C) 1/1
(D) इनमें से कोई नहीं

Answer ⇒ (B)

3. एक विद्युत द्विध्रुव के अक्ष पर r दूरी पर विद्युत क्षेत्र की तीव्रता E1 तथा लम्ब-अर्द्धक रेखा पर r दूरी पर तीव्रता E2 है। E1 एवं E2 के बीच का कोण 0 है। E1 : E2 एवं 0 होंगे।

(A) 1 : 1, π
(B) 1 : 2, π/2
(C) 2 : 1, π
(D) 1 : 3, π

Answer ⇒ (C)

4. आघूर्ण वाला एक विद्युतीय द्विध्रुव विद्युतीय क्षेत्र के साथ 90°का कोण बनाता है, तब इस पर लगा बल आघूर्ण –

^(A) X
^(B) .
(C) pE
(D) p/E

Answer ⇒ (A)

5. आघूर्ण वाला एक विद्युतीय द्विध्रुव विद्युतीय क्षेत्र के साथ 90° का कोण बनाता है, तब इस पर लगा बल आघूर्ण –

(A) pE
(B) zero
(C) 1/2pE
(D) 2pE

Answer ⇒ (A)

6. आघूर्ण वाला द्विध्रुव अधिकतम बल आघूर्ण तब अनुभव करेगा तथा के बीच कोण हो –

(A) 0°
(B) 90°
(C) 60°
(D) 30°

Answer ⇒ (B)

7. एक वैद्युत द्विध्रुव के केन्द्र से 100 cm की दूरी पर दो बिन्दु A तथा B स्थित हैं।A अक्षीय बिन्दु है जबकि B निरक्षीय। वैद्युत क्षेत्र की तीव्रता A पर तब B पर तीव्रता होगी –

(A)
(B) 2
(C) –
^{(D) –}

Answer ⇒ (D)

8. दो वैद्युत क्षेत्र रेखाएँ एक-दूसरे को किस कोण पर काटती हैं ?

(A) 90°
(B) 45°
(C) 30°
(D) नहीं काटती हैं

Answer ⇒ (D)

9. विद्युत आवेश का क्वांटम e.s.u.मात्रक में होता है

(A) 4.78 x 10^-10
(B) +1.6 x 10^-19
(C) 2.99 x 10⁹
(D) -1.6 x 10^-19

Answer ⇒ (A)

10. एक विधुतीय द्विध्रुव दो विपरीत आवेशों से बना है जिनके परिणाम +3.2 x 10^-19 C एवं -3.2 x 10^-19C हैं और उनके बीच की दूरी 2.5 x 10^-10 m है। विधुतीय द्विध्रुव का आघूर्ण है

(A) 7.68 x 10^-27 C m
(B) 7.68 x 10^-29 C m
(C) 7.86 x 10^-29 C m
(D) 7:86 x 10-²⁷ C m

Answer ⇒ (B)

11. स्थिर विधुतीय क्षेत्र होता है

(A) संरक्षी
(B) असंरक्षी
(C) कहीं संरक्षी तथा कहीं असंरक्षी
(D) इनमें से कोई नहीं

Answer ⇒ (A)

12. मूलबिन्दु पर एक धन बिन्दु आवेश Q स्थित है जबकि x = 2cm पर एक बिन्दु धन आवेश 2Q स्थित है –

(A) आवेशों के निकट x-अक्ष के बाहर स्थित बिन्दु पर वैद्युत क्षेत्र शून्य हो सकता है।
(B) आवशो के निकटx-अक्ष के बाहर स्थित बिन्दु पर वैद्युत क्षेत्र की तीवता हो सकती है।
(C) आवेशों के बीच किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता शून्य हो सकती है
(D) आवेशों के बाहर कुछ निश्चित बिन्दुओं पर क्षेत्र की तीव्रता शून्य हो सकती है,

Answer ⇒ (C)

13. एक वैद्युत द्विध्रुव को वैद्युत क्षेत्र में रखा जाता है जो y-अक्ष पर दिष्ट है, x-अक्ष की ओर जाने पर बदलता है पर y एवं z-अक्ष की ओर अचर रहता है। यदि द्विध्रुव x-अक्ष पर स्थित हो तो कुल बल –

(A) x-अक्ष की ओर होगा
(B) y-अक्ष की ओर होगा ।
(C) z-अक्ष की ओर होगा ।
(D) इनमें से कोई नहीं

Answer ⇒ (A)

14. एक ही पदार्थ के धातु के दो गोले A तथा B दिये गये हैं। एक पर +Q आवेश तथा दूसरे पर -Q आवेश दिया गया है

(A) A का द्रव्यमान बढ़ जाएगा
(B) B का द्रव्यमान बढ़ेगा ।
(C) द्रव्यमान पर कोई प्रभाव नहीं पड़ेगा
(D) इनमें से कोई नहीं

Answer ⇒ (B)

15. इलेक्ट्रॉन का विशिष्ट आवेश होता है –

(A) 1.8 x 10¹¹ C/kg
(B) 1.8 x 10^-19 C/kg
(C) 1.9 x 10^-19 C/kg
(D) इनमें से कोई नहीं

Answer ⇒ (A)

16. डिबाई मात्रक है –

(A) आवेश का
(B) विभव का
(C) विद्युत द्विध्रुव आघूर्ण का
(D) कोई नहीं

Answer ⇒ (C)

17. एक आवेशित चालक की सतह के किसी बिन्दु पर विद्युतीय क्षेत्र की तीव्रता

(A) शून्य होती है
(B) सतह के लंबवत् होती है
(C) सतह के स्पर्शीय होती है
(D) सतह पर 45° पर होती है

Answer ⇒ (B)

18. 1 कूलॉम आवेश बराबर होता है –

(A) 2.99 x 10⁹ e.s.u.
(B) 9 x 10⁹ e.s.u.
(C) 8.85 x 10^-12 e.s.u.
(D) इनमें से कोई नहीं

Answer ⇒ (A)

19. यदि गोले पर आवेश 10μC हो, तो उसकी सतह पर विद्युतीय फ्लक्स है

(A) 36π x 10⁴ Nm²/C
(B) 36π x 10^-4 Nm²/C
(C) 36π x 10⁶ Nm²/c
(D) 36π x 10^-6 Nm²/c

Answer ⇒ (C)

20. चित्र दर्शाता है कि दो आवेशों q₁ और q₂ के कारण विद्युत क्षेत्र रेखा पर आवेशों का बाहरी चिन्ह क्या है ?

(A) दोनों ऋणात्मक
(B) ऊपर धनात्मक तथा नीचे ऋणात्मक
(C) दोनों धनात्मक
(D) ऊपर ऋणात्मक और नीचे धनात्मक

Answer ⇒ (A)

21. एक पिण्ड पर आवेश लिखा जाता है Q = ne, जहाँ e = 1.6 x 10^-19 C जहाँ n के मान हैं

(A) 0, 2, 3, …….
(B) 0, ± 1, ± 2, 3, …..
(C) 0, -1, -2,-3, …..
(D) इनमें से कोई नहीं

Answer ⇒ (B)

22. एक विद्युत क्षेत्र में एक द्विध्रुव को X-अक्ष के समानान्तर रखा जाता है। द्विध्रुव पर बल

(A) शून्य होगा
(B) X-अक्ष पर लंब होगा
(C) X-अक्ष के अनु
(D) इनमें से कोई नहीं

Answer ⇒ (C)

23. एक विद्युत क्षेत्र में एक द्विध्रुव का आघूर्ण = pÎ है। इस पर लगता बल आघूर्ण होगा –

(A) z-अक्ष की ओर
(B) y-अक्ष की ओर
(C) x-अक्ष की ओर
(D) इनमें से कोई नहीं

Answer ⇒ (A)

24. X-अक्ष पर x = 0 पर q तथा x = a पर 2q आवेश रखे हैं। E का मान शून्य होगा –

(A) 0 < x < a
(B) x > a
(C) x < 0
(D) x < a

Answer ⇒ (C)

25. X-अक्ष पर x = 0 पर q तथा x = a पर 2q आवेश रखे हैं। आवेश q से N₁ तथा आवेश 2q से N2 क्षेत्र रेखाएँ निकलती हैं। तब होगी –

(A) 1
(B) 2
^(C)
(D) 4

Answer ⇒ (C)

26. किसी वस्तु पर आवेश की न्यूनतम मात्रा कम नहीं हो सकती।

(A) 1.6 x 10^-19 C
(B) 3.2 x 10^-19 C
(C) 4.8 x 10^-19 C
(D) 1 C

Answer ⇒ (A)

27. जब कोई वस्तु ऋणावेशित हो जाती है तो इसका द्रव्यमान क्या होता है।

(A) घटता है
(B) बढ़ता है
(C) वही रहता है
(D) इनमें से कोई नहीं

Answer ⇒ (B)

28. किसी वस्तु पर आवेश का कारण है।

(A) न्यूट्रॉन का स्थानांतरण
(B) प्रोटॉन का स्थानांतरण
(C) इलेक्ट्रॉन का स्थानांतरण
(D) प्रोटॉन तथा न्यूट्रॉन दोनों का स्थानांतरण

Answer ⇒ (C)

29. विद्युतीय क्षेत्र का विमीय सूत्र है

(A) [MLT^-3 A^-1]
(B) [ML² TA^-1]
(C) [MLT² A^-1]
(D) [MLTA²]

Answer ⇒ (A)

30. 1 स्टैट कूलाम =………. कूलाम।

(A) 3 x 10⁹
(B) 3 x 10^-9
^(C) ^{x 109}
^(D) ^{x 109}

Answer ⇒ (D)

31. एक आवेशित चालक का क्षेत्र आवेश घनत्व σ है। इसके पास विद्युत क्षेत्र का मान होता है

(A) σ/ 2 ∈₀
(B) σ/ ∈₀
(C) 2σ/ ∈₀
(D) σ/ 3 ∈₀

Answer ⇒ (B)

32. 1 कूलॉम आवेश बराबर होता है –

(A) 3 x 10⁹ e.s.u.
(B) _9 x 10⁹ e.s.u.
(C) –8.85 x 10^-12 e.s.u.
(D) इनमें से कोई नहीं

Answer ⇒ (A)

33. किसी आवेशित खोखले गोलाकार चालक के भीतर विद्युतीय तीव्रता का मान होता है –

(A) E₀σ
(B) σ/E₀
(C) zero
(D) E₀/2

Answer ⇒ (C)

34. वायु में एक-दूसरे से 30 cm की दूरी पर स्थित दो आवेशित कणों के आवेश क्रमश: 2 x 10-7 C तथा 3 x 10^-7 C हैं। इनके बीच लगते बल का परिणाम है –

(A) 6 mN
(B) 8 mN
(C) 10 mN
(D) इनमें से कोई नहीं

Answer ⇒ (A)

35. राशि ^,जहाँ संकेत सामान्य हैं, का विमीय सूत्र है।

(A) [MLT^-1 A^-1]
(B) [ML²T^-3 A^-1]
(C) [M°L°T°A°]
(D) [ML°T°A]

Answer ⇒ (C)

36. एक समान वैद्युत क्षेत्र में तीन पथ चिह्न I, II एवं III दिखाये गये हैं –

(A) पथचिह्न I धनावेशित कण का है
(B) पथचिह्न II ऋणावेशित कण का है
(C) पथचिह्न III उदासीन कण का है
(D) पथचिह्न III धनावेशित कण का है

Answer ⇒ (D)

37. कूलम्ब बल है –

(A) केन्द्रीय बल
(B) विद्युत बल \
(C) दोनों (A) तथा (B)
(D) इनमें से कोई नहीं

Answer ⇒ (C)

38. आघूर्ण वाला एक विद्युत द्विध्रुव तीव्रता वाले विद्युतीय क्षेत्र में रखा जाए, तो उस पर लगने वाला टार्क होगा

^(A) x
^(B) .
(C) pE
^(D)

Answer ⇒ (A)

39. एक वैद्युत द्विध्रुव से 100 cm की दूरी पर दो बिन्दु A तथा B स्थित हैं। A अक्षीय बिन्दु है जबकि B लम्बवत् द्विभाजक है। वैद्युत क्षेत्र की तीव्रता A पर तब B पर तीव्रता होगी –

(A)
(B) 2
(C) –
^(D) ^–

Answer ⇒ (D)

40. किसी आवेशित बेलन के नजदीक किसी बिन्दु पर विद्युत् तीव्रता E का मान होता है –

^(A)
^(B)
^(C)
(D) शून्य

Answer ⇒ (B)

41. एक विद्युत् द्वि-ध्रुव एक पृष्ठ से घिरा हुआ है। पृष्ठ पर कुल फ्लक्स होगा –

(A) अनंत
(B) शून्य
(C) आवेश पर निर्भर
(D) द्विध्रुव की स्थिति पर निर्भर

Answer ⇒ (B)

42. किसी वस्तु पर 1 कूलम्ब आवेश तब संभव है जब उससे निकाले गए इलेक्ट्रॉनों की संख्या होगी –

(A) 6.25 x 10_-19
(B) 6.25 x 10¹⁹
(C) 6.25 x 10¹⁸
(D) 6.25 x 10^-10

Answer ⇒ (C)

43. किसी अनावेशित वस्तु पर एक कूलम्ब आवेश होने के लिए उसमें से निकाले गये इलेक्ट्रॉनों की संख्या होगी

(A) 6.25 x 10¹⁸
(B) 6.25 x 10¹⁸
(C) 6.023 x 10²³
(D) इनमें से कोई नहीं

Answer ⇒ (A)

44. एक वैद्युत द्विध्रुव एक पृष्ठ से घिरा हुआ है। पृष्ठ पर कुल विद्युत फ्लक्स होगा –

(A) अनंत
(B) शून्य
(C) q/∈₀
(D) इनमें से कोई नहीं

Answer ⇒ (B)

45. किसी आवेश से अनंत दूरी पर उस आवेश के कारण विद्युत क्षेत्र की तीव्रता होती है –

(A) अनंत
(B) शून्य
(C) 9 x 10⁹ Vm^-1
(D) इनमें से कोई नहीं

Answer ⇒ (B)

46. यदि दो आवेशों की दूरी बढ़ा दी जाये तो आवेशों के विद्युतीय स्थितिज उर्जा का मान –

(A) बढ़ जाएगा
(B) घट जाएगा
(C) अपरिवर्तित रहेगा
(D) बढ़ भी सकता है घट भी सकता है

Answer ⇒ (D)

47. किसी आवेशित गोलीय खोखले चालक के भीतर विद्युत तीव्रता होती है –

(A) अनंत
(B) शून्य
(C) धनात्मक एवं 1 से अधिक
(D) इनमें से कोई नहीं

Answer ⇒ (B)

48. फ्लक्स घनत्व का मात्रक होता है –

(A) वेबर
(B) टेसला
(C) न्यूटन / मी
(D) मी²/से

Answer ⇒ (B)

49. आवेश A एवं B एक-दूसरे को आकर्षित करते हैं। आवेश B एवं C भी एक-दूसरे को आकर्षित करते हैं। तब A एवं C-

(A) आकृष्ट होंगे
(B) प्रतिकर्षित होंगे
(C) एक-दूसरे को प्रभावित नहीं करेंगे
(D) और अधिक सूचना चाहिए

Answer ⇒ (B)

50. एक अनावेशित धातुकण को एक धनावेशित धातु प्लेट के नजदीक लाया जाता है। धातु कण पर विद्युतीय बल होगा –

(A) प्लेट की तरफ
(B) प्लेट से दूर
(C) प्लेट के समांतर
(D) इनमें से कोई नहीं

Answer ⇒ (A)

51. दो चालकों के बीच आवेश के वितरण से होने वाली ऊर्जा की हानि निर्भर करती है –

(A) विभवांतर के
(B) विभवांतर के वर्ग पर
(C) धारिता पर
(D) इनमें से कोई नहीं

Answer ⇒ (B)

52. एक बिन्दु आवेश (q) को एक-दूसरे बिन्दु आवेश Q के चारों तरफ वृत्ताकार पथ पर घुमाया जाता है। विद्युत क्षेत्र के द्वारा किया गया कार्य होगा –

(A) शून्य
(B) धनात्मक
(C) ऋणात्मक
(D) इनमें से कोई नहीं

Answer ⇒ (A)

53. आवेश का S.I. मात्रक होता है

(A) एम्पीयर (A)
(B) फैराड (F)
(C) वोल्ट (V)
(D) कूलम्ब (C)

Answer ⇒ (D)

54. आवेश की विमा है –

(A) [AT]
(B) [LAT]
(C) [AT^-1]
(D) [AT^-2]

Answer ⇒ (A)

55. इलेक्ट्रॉन पर आवेश बराबर होता है –

(A) 2 x 10^-21 C
(B) 1.6 x 10^-19 C
(C) 1.6 x 10^-20 C
(D) इनमें से कोई नहीं

Answer ⇒ (B)

56. निम्नलिखित में किसका अस्तित्व संभव नहीं है –

(A) 3.2 x 10^-19 C
(B) 6.4 x 10^-19 C
(C) 2.4 x 10^-19 C
(D) 1.6 x 10^-19 C

Answer ⇒ (C)

57. स्थिर विद्युत् आवेशों के बीच लगता बल किस नियम से दिया जाता है ?

(A) गॉस का प्रमेय
(B) किरचॉफ के नियम
(C) कूलम्ब के नियम
(D) फैराडे के नियम

Answer ⇒ (C)

58. दो आवेशों के बीच की दूरी दुगुनी करने के बीच का बल –

(A) दुगुना हो जाता है
(B) आधा हो जाता है
(C) चार गुना हो जाता है
(D) चौथाई हो जाता है

Answer ⇒ (D)

59. 1 कूलम्ब वह आवेश है जो शून्य में 1 मीटर की दूरी पर स्थित समान आवेश पर बल लगाता है –

(A) 1 N
(B) 9 x 10^-9N
(C) 9x 10⁹N
(D) इनमें से कोई नहीं

Answer ⇒ (C)

60. मुक्त आकाश (Free space) की परावैद्युतता (∈₀) होती है –

(A) 9 x 10⁹ mF^-1
(B) 1.6 x 10^-19 C
(C) 8.85 x 10^-12 Fm^-1
(D) इनमें से कोई नहीं

Answer ⇒ (C)

61. राशि ^{का मान होता है}

(A) 9 x 10₉ Nm²C-²
(B) 8.85 x 10^-12 Nm²C^-2
(C) 9 x 10^-9 Nm²C^-2
(D) शून्य

Answer ⇒ (A)

62. किसी माध्यम की आपेक्षिक परावैद्युतता (∈ _r) बराबर होती है –

^(A)
(B) ∈ x ∈₀
(C) ∈ + ∈₀
(D) ∈ – ∈₀

Answer ⇒ (A)

63. विद्युतशीलता (x) का मात्रक होता है –

(A) न्यूटन/मी० Nm^-1
(B) फैराडे/मी० Fm^-1
(C) कूलम्ब/वोल्ट CV^-1
(D) इनमें से कोई नही

Answer ⇒ (B)

64. किसी विद्युतीय क्षेत्र में किसी बिन्दु पर परीक्षण आवेश (test charge) q₀ पर लगा विद्युत् बल हो तो उस बिन्दु पर विद्युत् तीव्रता () होगी।

^(A) =
^(B) = q₀
^(C) =
^(D) =q²₀F

Answer ⇒ (A)

65. विद्युत् क्षेत्र की तीव्रता (Electric field intensity) का मात्रक होता है –

(A) न्यूटन/कूलम्ब (NC)
(B) न्यूटन/कूलम्ब (NC^-1)
(C) वोल्ट/मी० (Vm)
(D) कूलम्ब/न्यूटन (CN^-1)

Answer ⇒ (B)

66. विद्युत् क्षेत्र की तीव्रता की विमा है –

(A) [MLT^-2 A^-1]
(B) [MLT^-3 A^-1]
(C) [ML2T^-3 A^-2]
(D) [ML²T²A²]

Answer ⇒ (A)

67. समरूप विद्युत् क्षेत्र की तीव्रता हो तब इसमें रखे गए +q आवेश पर लगा बल होगा –

(A) = q

^(B) ⁼

^(C) = q²
(D) इनमें से कोई नहीं

Answer ⇒ (A)

68. एक बिन्दु-आवेश Q से r दूरी पर विद्युत्-क्षेत्र की तीव्रता का परिणाम होता है –

Answer ⇒ (B)

69. एक प्रोटॉन एवं इलेक्ट्रॉन को समान विद्युत्-क्षेत्र में रखा जाता है –

(A) उन पर लगा विद्युत् बल बराबर होंगे
(B) विद्युत् बलों के परिणाम बराबर होंगे
(C) उनके त्वरण बराबर होंगे
(D) उनके त्वरण के परिणाम बराबर होंगे

Answer ⇒ (B)

70. निम्नलिखित में कौन सदिश राशि है ?

(A) आवेश
(B) धारिता
(C) विद्युत्-तीव्रता
(D) इनमें से कोई नहीं

Answer ⇒ (C)

71. विद्युत्-विभव का मात्रक वोल्ट है और यह तुल्य है –

(A) जूल/कूलम्ब
(B) जूल x कूलम्ब
(C) कूलम्ब/जूल
(D) इनमें से कोई नहीं

Answer ⇒ (A)

72. साबुन के एक बुलबुले को जब आवेशित किया जाता है तो उसकी त्रिज्या –

(A) बढ़ती है
(B) घटती है
(C) अपरिवर्तित रहती है।
(D) शून्य हो जाता है

Answer ⇒ (A)

73. विद्युत् द्वि-ध्रुव आघूर्ण का S.I. मात्रक होता है।

(A) कूलम्ब x मी० (C x m)
(B) कूलम्ब / मीटर C/ m
(C) कूलम्ब-मी०-² (C x m²)
(D) कूलम्ब² x मीटर (C² m)

Answer ⇒ (A)

74. पाँच विद्युतीय द्विध्रुव, जो प्रत्येक±qआवेश से बना है। दूरी से पृथक् है, घिरे पृष्ठ में रखा जाता है। पृष्ठ के ऊपर कुल फ्लक्स होगा –

(A) 10π q
(B) 20π q
(C) 5π 9
(D) शून्य

Answer ⇒ (D)

75. तीन बिन्दुओं 4g, Q तथा q एक सरल रेखा पर क्रमशः 0, 1/2 तथा 1 दूरी पर रखे हैं। यदि आवेश q पर परिणामी बल शून्य है तो Q का मान होगा –

(A) -q
(B) -2q
(C) -q/2
(D) 4q

Answer ⇒ (A)

76. एक समान विद्युत् क्षेत्र में द्विध्रुव पर आरोपित बल युग्म आघूर्ण अधिकतम है जबकि द्विध्रुव की अक्ष तथा क्षेत्र की दिशा के बीच का कोण है –

(A) शून्य
(B) 90°
(C) 180°
(D) 45°

Answer ⇒ (B)

77. यदि किसी अल्प क्षेत्र dA पर विद्युतीय तीव्रताअभिलम्ब हो, तब उस क्षेत्र पर ट विद्युत् फ्लक्स होगा –

(A) E . dA
(B) शून्य
(C) EdA cos0
(D) EdA sin0

Answer ⇒ (A)

78. किसी घिरे सतह पर कुल विद्युत् फ्लक्स पृष्ठ के भीतर स्थिर कुल आवेश का –

(A) 1/∈₀ गुना
(B) 1/4π गुना
(C) ∈₀ गुणा
(D) शून्य होता है

Answer ⇒ (A)

79. किसी आवेशित समतल चादर के नजदीक विद्युत् तीव्रता E का मान होता है –

(A) σ/∈₀
(B) σ/2∈₀
(C) σ x ∈₀
(D) शून्य

Answer ⇒ (B)

80. किसी आवेशित चालक के नजदीक विद्युत् तीव्रता का मान होता है –

(A) σ/∈₀
(B) σ/2∈₀
(C) σ x ∈₀
(D) शून्य

Answer ⇒ (A)

81. किसी अचालक पदार्थ के गोले को आवेश देने पर वह वितरित होता है –

(A) सतह पर
(B) सतह के अलावा अंदर भी
(C) केवल भीतर
(D) इनमें से कोई नहीं

Answer ⇒ (D)

82. चित्रानुसार बिन्दु A, B तथा C पर तीव्रता क्रमशः E_A, E_B तथा E_C हो तो –

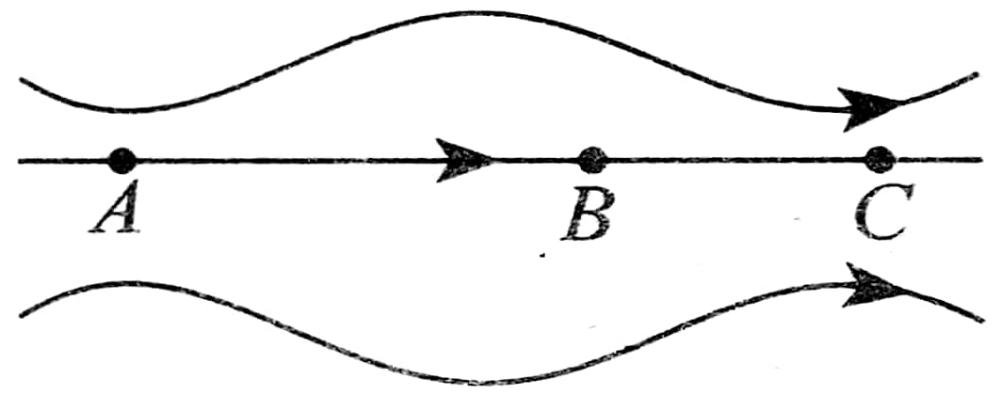
(A) E_A > E_B > E_c
(B) E_A = E_B = E_c
(C) E_A = E_C > E_B
(D) E_A = E_C = E_B

Answer ⇒ (C)

83. चालक पदार्थ से बने असीमित आवेशित पतली चादर की सतह के निकट स्थित किसी बिन्दु पर विद्युतीय क्षेत्र का मान होता है –

(A) ∈₀σ
(B) σ/∈₀
(C) σ/2∈₀
(D) 1/2 σ∈₀

Answer ⇒ (B)

84. दिए गये चित्र में, यदि आवेश Q पर कुल प्रभावी बल शून्य है, तो Q/q का मान है –

^(A)
^(B)
^(C)
^(D)

Answer ⇒ (B)

85. जब किसी वस्तु को आवेशित किया जाता है, तो उसका द्रव्यमान –

(A) बढ़ता है
(B) घटता है
(C) अचर रहता है
(D) बढ़ या घट सकता है

Answer ⇒ (D)

लघु उत्तरीय प्रश्न

1. आवेश का संरक्षण सिद्धान्त क्या है ? समझाएँ।

Ans ⇒ आवेश का संरक्षण सिद्धान्त – “किसी संकाय का कुल आवेश नियत होता है।अर्थात् आवेश न तो नष्ट किया जा सकता है और न ही इनकी सृष्टि की जा सकती है। किसी भी प्रक्रिया के पहले निकाय का जो नेट आवेश होता है, वही प्रक्रिया के बाद भी रहता है। यही आवेश का संरक्षण सिद्धान्त है।

2. विद्युत क्षेत्र तथा उसकी तीव्रता से आप क्या समझते हैं ?

Ans ⇒ विद्युत क्षेत्र – विद्युत क्षेत्र किसी आवेश के चारों तरफ का वह आकाश है जहाँ विद्युत बल का अनुभव किया जा सकता है। एक-दूसरे से r दूरी पर स्थित दो आवेश q तथा q₀ के बीच पारस्परिक क्रिया इस प्रकार होती है कि आवेश q₀ अपने चारों तरफ एक विद्युत क्षेत्र उत्पन्न करता है,
जिसका अस्तित्व दूसरे आवेशों की उपस्थिति से मुक्त होता है। उपस्थिति की जॉच भी होती है जब एक दूसरे आवेश q₀ इस क्षेत्र में लाया जाता है। आवेश q₀ का क्षेत्र जाँच–आवेश से पारस्परिक क्रिया कर विद्युत बल उत्पन्न करता है। बल का परिमाण दोनों आवेशों के बीच की दूरी पर निर्भर करता है। आवेश q के कारण r दुरी पर स्थित विधुत क्षेत्र की तीव्रता है, जहाँ आवेश q के कारण q₀ पर लगता हुआ बल है।
इस प्रकार विद्युत क्षेत्र में किसी बिन्दु पर एकांक धनावेश पर क्रियाशील बल को उसकी तीव्रता कहते हैं। विद्युत तीव्रता एक सदिश राशि है। इसकी दिशा बल की दिशा होती है।

विद्युत क्षेत्र की तीव्रता, E का S.I. मात्रक न्यूटन/ कूलम्ब है।

3. विद्युत द्विध्रुव तथा द्विध्रुव आघूर्ण क्या है ?

Ans ⇒ विद्युत द्विध्रुव – दो बराबर तथा विपरीत बिन्दु आवेश के किसी अल्प दूरी पर स्थित होने की स्थिति में उस निकाय को विद्युत द्विध्रुव कहते हैं।

द्विधव आघूर्ण – किसी विद्युत द्विध्रुव का द्विध्रुव आघूर्ण किसी एक आवेश का मान तथा दोनों आवेशों के बीच की दूरी का गुणनफल है।
माना कि 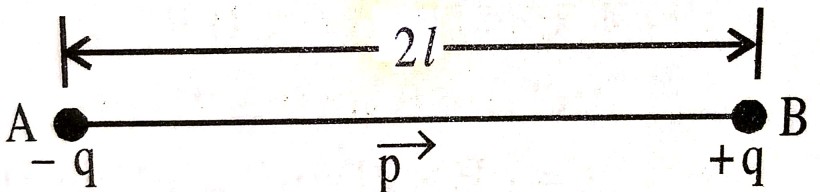A तथा B बिन्दु पर स्थित दो आवेश (-q) तथा (+q) परस्पर 2l दूरी पर स्थित हैं, तो उस विद्युत द्विध्रुव का द्विध्रुव

आघूर्ण, P = q x 2l = 2ql है। यह एक सदिश राशि है। इसकी दिशा द्विध्रुव की अक्ष के अनुदिश ऋण आवेश से धन आवेश की तरफ होती है। इसका मात्रक कूलम्ब-मीटर तथा विमीय सूत्र [M⁰L/T] है।

4. विद्युत क्षेत्र की तीव्रता तथा विभव में सम्बन्ध स्थापित करें।

Ans ⇒ विद्युत क्षेत्र की तीव्रता तथा विभव में सम्बन्ध – माना कि A तथा B दो बिन्दु अत्यल्प दूरी Δr से अलग हैं जिनके बीच विभवान्तर AV तथा विद्युत क्षेत्र की तीव्रता E है। आवेश q0 को B से A तक लाने में संपादित कार्य ΔW है, तो हम पाते हैं कि
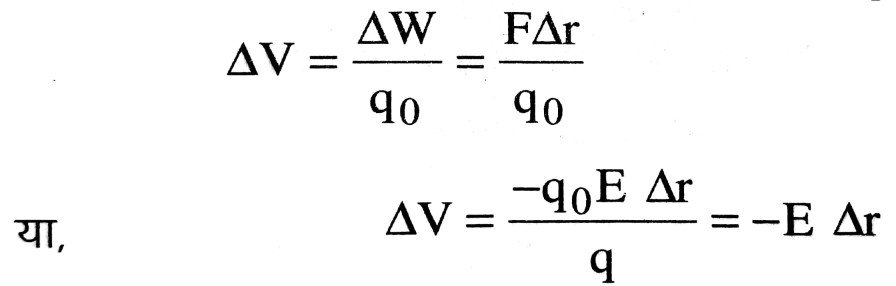क्योंकि F = -q₀E है, जहाँ q₀ के विरुद्ध बल F को लगाना नितांत आवश्यक है।

अतः विद्युत क्षेत्र में किसी बिन्दु पर किसी दिशा में उसकी तीव्रता का घटक उस दिशा में ऋणात्मक विभव प्रवणता के बराबर है। ऋणात्मक चिह्न यह बताता है कि विद्युत क्षेत्र की तीव्रता E तक धनात्मक होता है जब dV/dr ऋणात्मक होता है। विद्युत तीव्रता का मात्रक वोल्ट/मीटर है।

5. समविद्युत् क्षेत्र में विद्युत द्विध्रुव पर लगने वाले बलयुग्म का व्यंजक प्राप्त करें।

Ans ⇒ बलयुग्म का व्यंजक – माना कि एक विद्युत द्विध्रुव AB है जिसका आवेश -q व +q कूलम्ब है तथा इनके बीच की दूरी 21 है। द्विध्रुव एकसमान विधुत क्षेत्र E में विद्युत क्षेत्र की दिशा से कोण 0 बनाते हैं। विद्युत क्षेत्र E के कारण +q आवेश पर बल F = qE (विद्युत क्षेत्र E की दिशा में) तथा q आवेश पर बल F = qE (विद्यत क्षेत्र E की दिशा के विपरीत दिशा में लगता है)
चूकि ये दोनों बल परस्पर बराबर तथा विपरीत हैं। अतः इनका परिणामी बल शून्य है। लेकिन ये दोनों बल एक बलयुग्म बनाते हैं जो द्विध्रुव को घुमाकर विद्युत क्षेत्र E की दिशा में लाने का प्रयत्न करता है। इस प्रत्यानयन बलयुग्म का आघूर्ण

τ = बल x लम्बवत् दूरी = qE x BC
लेकिन समकोण Δ/_i CB में,
BC = ABsinθ = 2lsinθ
∴ τ = qE x 2lsinθ = pEsinθ (क्योंकि q x 2l = p)

6. कूलम्ब के प्रमेय को लिखें तथा प्रमाणित करें।
अथवा, आवेशित समतल चालक के नजदीक किसी बिन्दु पर विद्युतीय तीव्रता का व्यंजक ज्ञात करें।
अथवा, प्रमाणित करें कि है, जहाँ σ आवेश का तलीय घनत्व, ε₀ वायु की विद्युतशीलता तथा K माध्यम की पराविधुत स्थिरांक है।

Ans ⇒ कुलम्ब के प्रमेय – किसी आवेशित समतल चालक के बाहर किसी बिन्दु पर विद्युतीय तीव्रता, उसके तलीय घनत्व का 4π/K गुणा है, जहाँ K माध्यम का पराविद्युत स्थिरांक है।
अथवा, “किसी आवेशित समतल चालक के बाहर किसी बिन्दु पर विद्युतीय तीव्रता आवेश के तलीय घनत्व तथा वायु की विद्युतशीलता ε₀ का अनुपात होता है।

प्रमाण – माना कि x एक समतल चालक है, जिसका तलीय घनत्व AB समल पर σ है, जो K पराविद्युत स्थिरांक के माध्यम में है। ε₀ इसके वायु में विद्युतशीलता है। 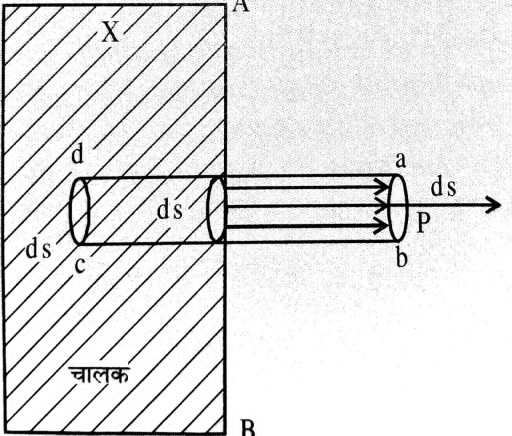P बिन्दु चालक के बाहर तथा नजदीक है जिस पर विद्यतीय तीव्रता का मान ज्ञात करना है।अब ds अनुप्रस्थ–परिच्छेद का वैसा बेलन खींचा जिसमें ab तथा cd, AB के समानान्तर है। P, AB समतल में ab तथा cd पर है । विद्युतीय बल रेखाएँ अर्थात् विद्युतीय फ्लक्स AB के अभिलम्बवत् है, तब बेलन के वक्र समतल पर अभिलम्ब विद्युत प्रेरण = 0 (शून्य) होता है।

∴ P बिन्दु पर अभिलम्ब विद्युत प्रेरण = K x P बिन्दु पर विद्युतीय तीव्रता x ab का क्षेत्रफल।
= KE ds या, E. ds

पराविद्युत स्थिरांक के वायु में होने की स्थिति में K = 1
∴ E = 4πσ होता है।

7. समान रूप से आवेशित गोला के कारण किसी बिन्दु पर विद्युतीय तीव्रता का व्यंजक प्राप्त करें।

Ans ⇒ आवेशित गोला के कारण किसी बिन्दु के लिए विद्युतीय तीव्रता का व्यंजक
(a) जब आवेशित चालक के बाहर बिन्दु स्थित हो :मान लिया कि R त्रिज्या तथा O केन्द्र का एक गोला है जिसे +q आवेश से आवेशित किया गया है । O से r दूरी पर स्थित P एक बिन्दु है। O केन्द्र के साथ r त्रिज्या का एक गोला B खींचा।
∴ B गोला का क्षेत्रफल = 4πr²
माना कि P बिन्दु पर विद्युतीय तीव्रता E है।
∴ B तल पर कुल विद्युतीय तीव्रता फ्लक्स = E x 4πr²
गॉस के प्रमेय से, कुल विद्युतीय फ्लक्स सतह के अन्दर कुल आवेशों तथा निर्वात की विद्युतशीलता के अनुपात के बराबर होता है।

(b) जब P बिन्दु आवेशित चालक की सतह पर हो :
इस स्थिति में, r = R
अत:

(c) जब बिन्दु आवेशित चालक के अन्दर है –
गोला के अन्दर कोई आवेश नहीं होता है।
∴ E = 0

8. गॉस के प्रमेय की सहायता से आवेश की समतल चादर के समीप विद्युत क्षेत्र की तीव्रता का व्यंजक प्राप्त करें।

Ans ⇒ मान लिया कि एक समतल चादर AB है जिस पर आवेश का पृष्ठ घनत्व σ है । इस समतल चादर के समीप कोई बिंदु P है जहाँ विद्युत क्षेत्र की तीव्रता E का मान ज्ञात करना है।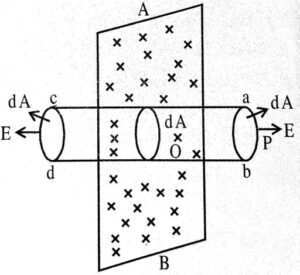

समतल चादर के पृष्ठ के लंबवत एक बेलनाकार तल abcd की कल्पना करें जिसका अक्ष तल के लंबवत है तथा सिरे ab और cd चादर के पृष्ठ के समानांतर है। लिया गया बिन्दु P पृष्ठ ab पर स्थित है।
अब चूंकि विद्युत तीव्रता की दिशा AB के लंबवत अर्थात् बेलन abcd के अक्ष के समानांतर है, अतः विद्युत फ्लक्स का योगदान केवल बेलन के समतल सिरों (ab और cd) पर होगा। यदि हो, तो ab और cd सिरों पर विद्युत फ्लक्स = EdA + EdA = 2EdA
अतः बेलनाकार तल पर कुल विद्युतीय फ्लक्स = 2 EdA
अब, चूँकि इस बेलनाकार तल के अंदर आवेश की समतल चादर dA क्षेत्रफल स्थित है इसलिए बेलनाकार तल के भीतर कुल आवेश σdA होगा। अतः गॉस के प्रमेय से तल पर कुल विद्युत फ्लक्स

9. विद्युत आवेश का क्वाण्टीकरण क्या है ?

Ans ⇒ आवेशों का क्वाण्टीकरण (Quantised electric charge)- प्रत्येक पदार्थ सामान्य रूप में आवेशहीन होता है, परन्तु इन पर आवेशों का आदान-प्रदान इलेक्ट्रॉन के रूप में करने पर ये आवेशित होते हैं। अतः किसी पिण्ड पर आवेश Q = ±ne होता है।
जहाँ n = 1, 2, 3, … अर्थात् पूर्णांक संख्या होगी न कि अपूर्णांक संख्या।
अतः किसी पिण्ड पर आवेश का परिमाण हमेशा electric charge (e) का पूर्णांक संख्या के गुणक के रूप में होता है।
यही आवेशों का क्वाण्टीकरण कहलाता है।

10. एकांक आवेश या एक कूलाम्ब आवेश को परिभाषित करें।

Ans ⇒ एकांक आवेश या एक कूलाम्ब आवेश (Unit charge or charge of one coulomb) – माना कि q1 तथा q2 परिमाण के दो आवेश हवा में एक- दूसरे से एक मीटर की दूरी पर रखे गये हैं। कूलाम्ब के नियम से इनके बीच लगा विद्युतीय विकर्षण बल्ब

“अतः अगर हवा में एक मीटर की दूरी पर स्थित दो आवेशों के बीच 9 x 10⁹ N का विकर्षण बल लगता हो तब प्रत्येक आवेश को 1 कूलाम्ब का आवेश या एकांक आवेश कहा जाता है।”

11. क्या विद्युतीय क्षेत्र एक संरक्षी बल है ?

Ans ⇒ संरक्षी बल वह बल होता है जिसके प्रभाव में दो बिन्दुओं के बीच सम्पादित कार्य केवल उसके प्रारंभिक तथा अंतिम बिन्दु पर निर्भर करता है, तय किए गए पथ से स्वतंत्र हो। या बल के प्रभाव में एक पूर्ण चक्र में किया गया कार्य शून्य हो।
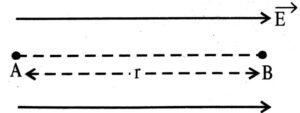माना कि समरूप विद्युतीय क्षेत्र में r दूरी पर A तथा B दो बिन्दु हैं। अत: A से B तक एकांक धन आवेश को लाने में किया गया कार्य

12. विद्युतीय बल रेखाएँ क्या हैं ? इसके मुख्य गुण क्या है ?

Ans ⇒ विद्युत बल रेखाएँ (Electric line of forces) – किसी क्षेत्र में विद्युतीय बल रेखाएँ वे काल्पनिक रेखाएँ हैं जिस पथ पर कोई स्वतंत्र एकांक धन आवेश बंद करता है।
विद्युतीय बल रेखाओं के गुण –
(i) विद्युतीय बल रेखाएँ +ve आवेश से निकलती हैं तथा –ve आवेश पर बन्द होती है। (ii) विद्युतीय बल रेखाओं के प्रत्येक बिन्दु पर खींची गई स्पेर्श रेखा के दिशा में विद्युतीय क्षेत्र की दिशा होती है।
(iii) दो विद्युतीय बल रेखाएँ एक-दूसरे को नहीं काटती है।

13. मुक्त अवस्था की विद्युतशीलता का मात्रक एवं विमा लिखें।

Ans ⇒ विद्युतशीलता का SI मात्रक C²N^-1m^-2 है। विद्युतशीलता की विमा [M^-1L^-3T⁴A²] है।

14. किसी गॉसीय पृष्ठ में (-q), (+2q) तथा (-q) आवेश हैं। पृष्ठ में से परिणामी विद्युत फ्लक्स की गणना करें।

Ans ⇒ गौसीय पृष्ठ के अन्दर कुल आवेश Q = (-q) + (+2q) + (-q) = 0 (Zero)
∴ विद्युत क्षेत्र E = 0
∴ विद्युत फ्लक्स = φ =
= 0. = 0 (zero)

15. (a) स्थिर वैद्युत क्षेत्र रेखा पर संतत वक्र होती है अर्थात् कोई क्षेत्र रेखा एकाएक नहीं टूट सकती। क्यों ?
(b) स्पष्ट कीजिए कि दो क्षेत्र रेखाएँ कभी भी एक-दूसरे का प्रतिच्छेदन क्यों नहीं करतीं ?

Ans ⇒ (a) किसी बिन्दु पर स्थिर विद्युत बल रेखा वह पथ है जिसके प्रत्येक बिन्दु पर स्पर्शज्या उस बिन्दु पर विद्युत क्षेत्र की दिशा बताती है। विद्युत-क्षेत्र की दिशा एक बिन्दु से दूसरे बिन्दु पर बदल जाती है। अतः बल रेखाएँ आमतौर पर वक्र रेखाएँ होती हैं। इसके अतिरिक्त वह सतत वक्र
होती हैं जो अचानक नहीं टूटती क्योंकि यदि ऐसा है तो टूटने के स्थान पर यह कोई विद्युत क्षेत्र नहीं दर्शाएँगी।

(b) विद्युत-बल रेखाएँ एक-दूसरे को नहीं काटती क्योंकि यदि ऐसा है तो काट बिन्दु पर हम दो स्पर्शज्याएँ खींच सकते हैं जो उस बिन्द पर विद्युत क्षेत्र की दो दिशाएँ दर्शाएँगी जो संभव नहीं है।

16. चित्र में दर्शाए गए वक्र स्थिर वैद्युत क्षेत्र रेखाएँ निरूपित करता है या नहीं ?
Ans ⇒ यह चित्र वैद्युत बल रेखाएँ दर्शाता है। इसमें बिन्दु आवेश लिए हैं।

17. चित्र में किसी एकसमान स्थिर वैद्यत क्षेत्र में तीन आवेशित कणों के पथचिह्न (Tracks) दर्शाए गए हैं। तीनों आवेशों के चिह्न लिखिए। इनमें किस कण का आवेश संहति अनुपात अधिकतम है ?
Ans ⇒ चूँकि कण (1) और कण (2) धनावेशित प्लेट की ओर विक्षेपित होता है इसलिए इस पर ऋण आवेश है। कण (3) ऋणावेशित प्लेट की ओर विक्षेपित होता है इसलिए इस धन आवेश है।
कण (3) में विक्षेप अधिकतम होता है, इसलिए इस पर आवेश अधिकतम तथा द्रव्यमान न्यूनतम है। अतः कण (3) का आवेश संहति अनुपात अधिकतम है।

18. (a) किसी चालक A जिसमें चित्र में दर्शाए अनुसार कोई कोटर (cavity) है, को Q आवेश दिया गया है। दिखाएँ कि समस्त आवेश चालक के बाह्य पृष्ठ पर प्रतीत होना चाहिए।

(b) उपर्युक्त प्रश्न में अन्य चालक B जिसपर q आवेश है, कोटर में चित्रानुसार धंसा दिया जाता है कि B चालक A से विद्युतरोधी रहे। दिखाएँ कि चालक A के बाहरी सतह पर कुल आवेश Q + q है।

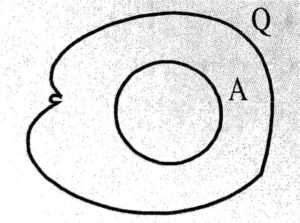
Ans ⇒ (a) माना कि चालक A के अन्दर में कोटर है जिसमें आवेश नही है। कोटर के घेरते हुए चालक के अन्दर गाउसीय सतह की कल्पना किया। गाउसीय सतह से जाने वाला विद्युत फ्लक्स φ = 0
q/ε = 0 ∴ q = 0
अतः चालक के अन्दर आवेश नहीं है। सम्पूर्ण आवेश चालक के बाहरी सतह पर है।

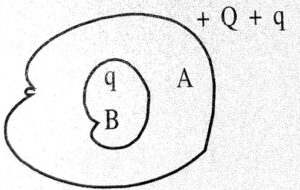
(b) जब कोटर में +q आवेश रखा जाता है तब प्रेरण से A के अन्दर के सतह पर -q आवेश उत्पन्न होता है तथा बाहरी सतह पर +q आवेश उत्पन्न होता है। कोटर के अन्दर कुल आवेश = 0
चालक A के बाहरी सतह पर कुल आवेश = Q + q.

(c) उपकरण को धात्विक पृष्ठ के पूर्णतः अन्दर रखा जा सकता है। ऐसा करने पर उपकरण विद्युत प्रभाव से परिरक्षित होता है क्योंकि धात्विक पृष्ठ के अन्दर स्थिर विद्युत क्षेत्र नहीं होता है। इस घटना को स्थिर विद्युत परिरक्षित कहते हैं।

19. (a) किसी यादृच्छिक स्थिरवैद्युत क्षेत्र विन्यास पर विचार कीजिए। इस विन्यास की किसी शून्य-विक्षेप स्थिति (null-point, अर्थात् जहाँ E = 0) पर कोई छोटा परीक्षण आवेश रेखा गया है। यह दर्शाइए कि परीक्षण का संतुलन आवश्यक रूप से अस्थायी है।
(b) इस परिणाम का समान परिणाम तथा चिहों के दो आवेशों (जो एक-दूसरे से किसी दूरी पर रखे हैं) के सरल विन्यास के लिए सत्यापन कीजिए।

Ans ⇒ (a) माना कि संतुलन स्थायी है। परीक्षण आवेश को शून्य विक्षेप स्थिति सेकिसी भी दिशा में थोड़ा विस्थापित करने पर शून्य विक्षेप स्थिति की ओर परीक्षण आवेश प्रत्यानयन बल अनुभव करेगा। अर्थात् शून्य विक्षेप स्थिति के समीप सभी विद्युत क्षेत्र रेखाएँ शून्य विक्षेप स्थिति के चारों ओर बंद सतह की कल्पना किया जाए तो बंद सतह से होकर नेट विद्युत फ्लक्स अन्दर की ओर होना चाहिए। परन्तु बंद सतह के भीतर ओवश नहीं हो तब विद्युत फ्लक्स शून्य होता है। अतः संतुलन स्थायी नहीं है।

(b) यदि परीक्षण आवेश को शून्य विक्षेप स्थिति Nसे दायें या बायें खिसकाया जाए तो इस पर प्रत्यानयन बल लगेगा। जो परीक्षण आवेश को N की ओर लायेगा। यदि परीक्षण आवेश को N के ऊपर या नीचे की ओर विस्थापित किया जाए तब इर पर विद्युत बल लगता है जो परीक्षण आवेश को N से दूर ले जायेगा । अतः परीक्षण आवेश हमेशा सभी दिशाओं में प्रत्यानयन बल का अनुभव नहीं करेगा। अतः परीक्षण आवेश का संतुलन अस्थायी है।

Leave a Comment Cancel Reply