Trigonometry

Trigonometric Ratio Formulas

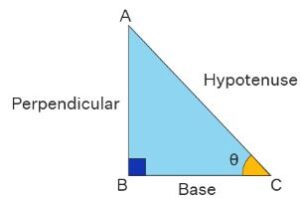
Sin θ = Perpendicular/Hypotenuse ( p/h)

Cos θ = Base/Hypotenuse (b/h)

Tan θ = Perpendicular/Base (p/b)

Sec θ = Hypotenuse/Base (h/b)

Cosec θ = Hypotenuse/Perpendicular (h/p)

Cot θ = Base/Perpendicular (b/p)

h² = p² + b²

p² = h² – b²

b² = h² – p² 

Reciprocal Identities

Sin θ = 1/cosec θ

Cosec θ = 1/sin θ

Cos θ = 1/sec θ

Sec θ = 1/cos θ

Tan θ = 1/cot θ

Cot θ = 1/tan θ

Pythagorean Identities

Sin²θ + Cos²θ = 1

Sec²θ – Tan²θ = 1

Cosec²θ – Cot²θ = 1

Tanθ = Sinθ/Cosθ

Cotθ = Cosθ/Sinθ

Trigonometric Functions in Four Quadrants 

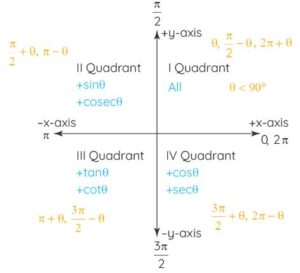
First Quadrant:

sin (π/2 – θ) = cos θ

cos (π/2 – θ) = sin θ

sin (2π + θ) = sin θ

cos (2π + θ) = cos θ

Second Quadrant:

sin (π/2 + θ) = cos θ

cos (π/2 + θ) = – sin θ

sin (π – θ) = sin θ

cos (π – θ) = – cos θ

Third Quadrant:

sin (π + θ) = – sin θ

cos (π + θ) = – cos θ

sin (3π/2 – θ) = – cos θ

cos (3π/2 – θ) = – sin θ

Fourth Quadrant:

sin (3π/2 + θ) = – cos θ

cos (3π/2 + θ) = sin θ

sin (2π – θ) = – sin θ

cos (2π – θ) = cos θ

Even and Odd Angle Formulas

sin(-θ) = – sinθ

cos(-θ) = cosθ

tan(-θ) = -tanθ

cot(-θ) = -cotθ

sec(-θ) = secθ

cosec(-θ) = – cosecθ

Co-function Formulas

sin(90⁰– θ) = cosθ

cos(90⁰– θ) = sinθ

tan(90⁰– θ) = cotθ

cot(90⁰– θ) = tanθ

sec(90⁰– θ) = cosecθ

cosec(90⁰– θ) = secθ

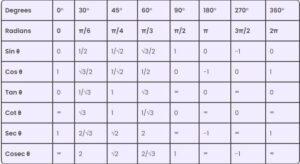
Trigonometric Table