समान्तर श्रेणियाँ (Arithmetic Progressions)
गणित में समान्तर श्रेणी (अंग्रेज़ी: Arithmetic progression) अथवा समान्तर अनुक्रम : संख्याओं का एक ऐसा अनुक्रम है जिसके दो क्रमागत पदो का अन्तर नियत होता है।
जैसे :- अनुक्रम 4, 7, 10, 13, 16 … एक समान्तर श्रेणी है जिसका सार्व अंतर 3 है।
अनुक्रम :- यदि किसी संख्या समूह को लिखने में एक निश्चित नियम का पालन किया गया हो, उसे अनुक्रम कहते हैं।
पदान्तर :- अनुक्रम मे दो क्रमागत पदो का अंतर पदांतर कहलाता है।
समान्तर श्रेढ़ी के प्रकार :-
1.परिमित समान्तर श्रेढ़ी – एक समान्तर श्रेढ़ी जिसमें परिमित संख्याएँ होती हैं उसे परिमित समान्तर श्रेढ़ी कहते हैं। इस प्रकार की समान्तर श्रेढ़ी में अंतिम पद होता है।
उदाहरण – 5, 10, 15, 20, 25, 30 ………………………….100 (अंतिम पद)।
2. अपरिमित समान्तर श्रेढ़ी – एक समान्तर श्रेढ़ी जिसमें अनंत संख्या में पद होते हैं उसे अपरिमित समान्तर श्रेढ़ी कहा जाता है। इस प्रकार की समान्तर श्रेढ़ी में अंतिम पद नहीं होता है।
उदाहरण – 10, 20, 30, 40, 50, 60 ……..
व्यापक रूप में भी लिखा गया है।
Tn = a + (n – 1)d
यहाँ, Tn = n वाँ पद या व्यापक पद
a = पहला पद
n = पदों की संख्या
d = सार्व अंतर
समान्तर श्रेढ़ी के पदों का चयन कैसे करें यदि नहीं दिए गए है तो –
यदि कोई प्रश्न है जिसमें न तो समान्तर श्रेढ़ी दी गई है और न ही कोई पद दिया गया है और हमें समान्तर श्रेढ़ी ज्ञात करनी है तो हमें पदों को एक अलग क्रम में चयन करना होगा। अलग क्रम में पदों को चयन करने से हमें आसानी से समान्तर श्रेढ़ी ज्ञात करने में सहायता मिलती है। आइए देखें कि पदों का चयन कैसे करे।
यदि हमें तीन पद मानने हैं तो पद हैं – a – d, a, a + d
यदि हमें चार पद मानने हैं तो पद हैं – a – 3d, a – d, a + d, a + 3d
यदि हमें पाँच पद मानने हैं तो पद हैं – a – 2d, a – d, a, a + d, a + 2d
यदि हमें छः पद मानने हैं तो पद हैं – a – 5d, a – 3d, a – d, a + d, a + 3d, a + 5d
कुछ लघुत्तरात्मक प्रश्न –
1.समान्तर श्रेढ़ी क्या है?
उत्तर – वह क्रम जिसमें प्रत्येक पद(पहले पद को छोड़कर) पूर्ववर्ती पद में एक निश्चित संख्या(धनात्मक या ऋणात्मक) जोड़कर प्राप्त किया जाता है, उसे समान्तर श्रेढ़ी कहा जाता है। उदाहरण – 1, 3, 5, 7, 9, ………
2. समान्तर श्रेढ़ी कितने प्रकार की होती है? नाम लिखो।
उत्तर – समान्तर श्रेढ़ी के दो प्रकार हैं।
( 1) परिमित समान्तर श्रेढ़ी
( 2) अपरिमित समान्तर श्रेढ़ी
3. समान्तर श्रेढ़ी के n वाँ पद (व्यापक पद) का सूत्र क्या है?
उत्तर – समान्तर श्रेढ़ी का n वाँ पद (व्यापक पद), tn = a + (n – 1)d
जहाँ, a = पहला पद, d = सार्व अंतर, n = पदों की संख्या, tn = n वाँ पद या व्यापक पद
4. समान्तर श्रेढ़ी के पहले n पदों के योग का सूत्र क्या है?
उत्तर – समान्तर श्रेढ़ी के पहले n पदों का योग, Sn = n/2[2a + (n – 1)d]
जहाँ, a = पहला पद, d = सार्व अंतर, n = पदों की संख्या, Sn = पहले n पदों का योग
5. परिमित समान्तर श्रेढ़ी के पहले n पदों के योग का सूत्र क्या है?
उत्तर – परिमित समान्तर श्रेढ़ी के लिए, पहले n पदों का योग, Sn = n/2[a + l ]
जहाँ, a = पहला पद, l = अंतिम पद, n = पदों की संख्या, Sn = पहले n पदों का योग
6. समान्तर श्रेढ़ी का व्यापक रूप क्या है?
उत्तर – समान्तर श्रेढ़ी का व्यापक रूप = a, a + d, a + 2d, a + 3d , …….a + (n – 1)d
7. प्राकृतिक संख्या का योग = ![]()
8. वर्गों का योग = ![]()
9. घन का योग = 
10. मध्य = 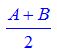
वस्तुनिष्ठ प्रश्न
1.समांतर श्रेणी -10, 6, -2, 2, का सार्व अंतर है :
(A) – 4
(B) 4
(C) 2
(D) इनमें से कोई नहीं
Ans :- B
2. यदि x + 2, 3x और 4x + 1 समांतर श्रेढ़ी में हो तो x का मान होगा :
(A) 1
(B) 2
(C) 3
(D) 4
Ans :- C
3. यदि किसी समांतर श्रेढ़ी का प्रथम पद 13 एवं सार्व- अंतर – 4 हो तो इसके प्रथम 10 पदों का योगफल होगा :
(A) 50
(B) -50
(C) 30
(D) -30
Ans :- B
4. समांतर श्रेढ़ी 14, 9, 4, -1, -6, ……. का 12वाँ पद है :
(A) 41
(B) -41
(C) 40
(D) 36
Ans :- B
5. समांतर श्रेढ़ी 0, -4,-8,-12 का सार्व अंतर है :
(A) 0
(B) 4
(C) -4
(D) 2
Ans :- C
6. समांतर श्रेणी 2, 7, 12, …… का प्रथम 10 पदों का योगफल होगा :
(A) 245
(B) 240
(C) 244
(D) 254
Ans :- A
7. समांतर श्रेणी 14, 9, 4, -1, – 6,…. का nवाँ पद होगा
(A) (19 + 5n)
(B) (19 – 5n)
(C) (19 + n)
(D) इनमें से कोई नहीं
Ans :- B
8. समांतर श्रेढ़ी 25, 20, 15….. का कौन-सा पद प्रथम ऋणात्मक पद है ?
(A) 6वाँ
(B) 7वाँ
(C) 8वाँ
(D) 9वाँ
Ans :- B
9. समांतर श्रेढ़ी 3/5 , 5/4 , 7/4 , 9/4 ………….का सार्व अंतर है :
(A) 3/4
(B) 1/4
(C) 1/2
(D) 5/4
Ans :- C
10. यदि समांतर श्रेढ़ी का nवाँ पद, an = 9 – 5n तो a7 =
(A) 26
(B) -26
(C) 45
(D) 2
Ans :- B
11. यदि समांतर श्रेढ़ी का सार्व अन्तर -2 है, तथा nवाँ पद an तो a17 – a13 =
(A) -2
(B) 4
(C) 8
(D) -8
Ans :- D
12. समांतर श्रेढ़ी 5, 8, 11, 14, ……का 12वाँ पद है :
(A) 35
(B) 38
(C) 41
(D) 238
Ans :- B
13. निम्नलिखित में कौन-सा समांतर श्रेढ़ी में नहीं है ?
(A) a, a +d, a + 2d, a + 3d,……
(B) √2, √8, √18, √32 ……..
(C) 0.3, 0.33, 0.333, 0.3333, …..
(D) ½ , 1/3 , 1/6 , 0 , ……
Ans :- C
14. A. P. 4, 10, 16, 22, 28 ……. का सार्व अन्तर होगा :
(A) 4
(B) 6
(C) 2
(D) 8
Ans :- B
15. जब A. P. के प्रथम पद 2 तथा सार्व अन्तर 3 हों, तब A.P के तीन पद होंगे:
(A) 2, 6, 9
(B) 2, 5, 8
(C) 2, 6,10
(D) 2, 5, 9
Ans :- B
16. यदि किसी A.P. का सामान्य पद 3n + 5 है तो इसका सार्व अन्तर होगा :
(A) 1
(B) 2
(C) 3
(D) 5
Ans :- C
17. यदि किसी A. P. का छठा और बारहवाँ पद क्रमशः 13 और 25 हैं, तो इसका 20वाँ पद है:
(A) 41
(B) 39
(C) 43
(D) 47
Ans :- A
18. अनुक्रम 5, 7, 9, 11, … का कौन सा पद 27 है?
(A) 13वाँ
(B) 12वाँ
(C) 11वाँ
(D) 10 वाँ
Ans :- B
19. 1, 5, 9, 13, 17, 21, 25……. समान्तर श्रेढ़ी में हैं, तो पदान्तर का मान होगा :
(A) 1
(B) 2
(C) 3
(D) 4
Ans :- D
20. निम्नलिखित में कौन समांतर श्रेणी में है ?
(A) 2, 4, 8, 16…
(B) -10, -6, -2, 2,…
(C) 3, 5, 4, 2…
(D) √3,√6, √9, √12…
Ans :- B
21. तीन संख्याएँ A.P में हैं तथा उनका योग 24 है। उनके वर्गों का योग 200 है, तो वे संख्याएँ हैं :
(A) 4, 8, 12
(B) 6, 8, 10
(C) 5, 8, 11
(D) 2, 8, 14
Ans :- B
22. 0 और 50 के बीच की विषम संख्याओं का योगफल होगा :
(A) 50
(B) 500
(C) 625
(D) कोई नहीं
Ans :- C
23. किसी A.P. की चार संख्याओं का योग 40 और उनके पहली और चौथी संख्याओं का गुणनफल 91 है, वे संख्याएँ हैं :
(A) 7, 9, 11, 13
(B) 6, 8, 12, 14
(C) 4, 7, 10, 19
(D) 3, 8, 9, 20
Ans :- A
24. स० श्रे० 10, 7, 4, …….का 30वाँ पद :
(A) 75
(B) -77
(C) 55
(D) 67
Ans :- B
25. स० श्रे० -3 , -1/2 , 2 , ………… का 11वाँ पद है :
(A) 22
(B) 30
(C) 25
(D) 32
Ans :- A
26. स० श्रे० 2, 7, 12, ……. का 10वाँ पद है :
(A) 50
(B) 40
(C) 47
(D) 53
Ans :- C
27. एक A. P. के 15 पदों का योग क्या है, जिसके प्रथम और अन्तिम पद क्रमश: 5 और 75 हैं?
(A) 550
(B) 500
(C) 600
(D) 700
Ans :- C
28. प्रथम 200 प्राकृत संख्याओं का योग हैं:
(A) 30600
(B) 20100
(C) 40200
(D) कोई नहीं
Ans :- B
29. 107 और 253 के बीच की 5 से विभाज्य संख्याओं का योग है :
(A) 5220
(B) 5210
(C) 5200
(D) 50000
Ans :- A
30. यदि A. P. का प्रथम पद a और d पदान्तर हो, तो nवॉ पद निम्नांकित कौन-सा होगा ?
(A) a + (n – 2 ) d
(B) a + (n-1)d
(C) a + nd
(D) a – (a – 1) d
Ans :- B
31. यदि A.P का प्रथम पद a और पदान्तर d हो, तो इसके प्रथम n पदों का योगफल निम्नांकित में कौन-सा होगा?
(A) a + (n – 1) d
(B) a + nd
(C) ![]()
(D) ![]()
Ans :- C
32. A.P. 5, 7, 9, 11, …….. के सातवाँ पद का मान होगा
(A) 20
(B) 25
(C) 17
(D) 35
Ans :- C
33. A.P. 21, 18, 15, …… का कौन पद शून्य है ?
(A) 7वाँ
(B) 8वाँ
(C) 9वाँ
(D) 10वाँ
Ans :- B
34. A. P. √2, √8, √18, √32 में पाँचवा पद है:
(A) √20
(B) √50
(C) √60
(D) √80
Ans :- B
35. A.P. 13, 19,…….., 205 के पदों की संख्या है :
(A) 30
(B) 31
(C) 32
(D) 33
Ans :- D
36. किसी A.P. का दूसरा पद 4 और साँतवा पद -11 है तो सार्वअन्तर होगा :
(A) 2
(B) 3
(C) -2
(D) -3
Ans :- D
37. यदि 4/5 , a , 2 किसी A.P. के तीन क्रमागत पद है तो a का मान होगा :
(A) 1/2
(B) 4/5
(C) 7/5
(D) 9/4
Ans :- C
38. समान्तर श्रेणी 2, 6, 10, 14, ………का कौन सा पद 82 है ?
(A) 15वाँ
(B) 20वाँ
(C) 21वाँ
(D) 22वाँ
Ans :- C
39. समान्तर श्रेणी 54 , 51, 48, 45, ……. का 10वाँ पद है:
(A) 27
(B) 30
(C) – 27
(D) इनमें कोई नहीं
Ans :- A
40. यदि p+1, 2p+1, 4p -1 AP, में है, तो P का मान है
(A) 1
(B) 2
(C) 3
(D) 4
Ans :- B
41. यदि किसी समान्तर श्रेणी का छठा और बारहवाँ पद 13 और 25 है, तो इसका पहला पद है :
(A) 4
(B) 3
(C) 2
(D) 5
Ans :- B
42. यदि 4 , x1 , x2 , x3 , 28 समांतर श्रेणी (AP) में है, तो x3 = ?
(A) 19
(B) 23
(C) 22
(D) ज्ञात नहीं किया जा सकता
Ans :- C
43. समांतर श्रेणी 72, 63, 54 ……..का कौन-सा पद शून्य है ?
(A) 8वाँ
(B) 9वाँ
(C) 10वाँ
(D) 11वाँ
Ans :- B
44. समांतर श्रेणी 21, 42, 63, 84 , ……… का कौन सा पद 210 है ?
(A) 9वाँ
(B) 10वाँ
(C) 11वाँ
(D) 12वाँ
Ans :- B
45. समांतर श्रेणी -40, -15, 10, 35 ……… का 10वाँ पद है
(A) 184
(B) 186
(C) 182
(D) 185
Ans :- D
46. 1 से 100 तक सभी प्राकृत संख्याओं का योग है।
(A) 4050
(B) 5050
(C) 6050
(D) 7050
Ans :- B
47. समान्तर श्रेणी 1, 4, 7, 10, …….. का कौन-सा पद 88 है?
(A) 26
(B) 27
(C) 30
(D) 35
Ans :- C
48. 1+ 2 + 3 + … + n बराबर है:
(A) n+1/2
(B) n(n+1)(n+2) / 2
(C) n(n+1) / 2
(D) n(n-1) / 2
Ans :- C
49. – 10, – 6, -2, 2,……, 34 में पदों की संख्या है
(A) 15
(B) 12
(C) 13
(D) 14
Ans :- B
50. समांतर श्रेणी 2, 7, 12, 17, ….. के लिए a30 – a20 का मान है (जहाँ an समांतर श्रेणी का nवाँ पद है ।)
(A) 100
(B) 10
(C) 50
(D) 20
Ans :- C
51. समान्तर श्रेणी 6, 13, 20, …….., 216 का मध्य पद है
(A) 118
(B) 104
(C) 111
(D) 125
Ans :- C
52. निम्नलिखित में कौन समान्तर श्रेणी में नहीं है ?
(A) 12, 52, 72, 73, …
(B) √2, √8, √18, √32,…
(C) -10, -6, -2, 2,..
(D) 0.2, 0.22, 0.222, 0.2222,…..
Ans :- D
53. यदि संख्याएँ (2x – 1), (3x + 2) तथा (6x – 1) समांतर श्रेणी में हो, तो x का मान है
(A) 3
(B) 1
(C) 2
(D) 0
Ans :- A
54. समांतर श्रेणी 5, 8, 11, 14 …… का दसवाँ पद है।
(A) 32
(B) 35
(C) 38
(D) 185
Ans :- A
55. समांतर श्रेढ़ी 3, 7, 11 ….. का 14वाँ पद है
(A) 52
(B) 55
(C) 56
(D) 59
Ans :- B
56. निम्नलिखित में कौन-सा समांतर श्रेढ़ी में है ?
(A) -8, -6, -4, -2, …
(B) 5, 15, 18, 28,
(C) 0.1, 0.11, 0.111, 0.1111….
(D) 1, ½ , 3/2 , 2 ……..
Ans :- A
57. समांतर श्रेढ़ी 16, 11, 6, 1, -4,……. का nवाँ पद होगा
(A) 21 + 5n
(B) 21- 5n
(C) 5n – 11
(D) 11 + 5n
Ans :- B
58. यदि समांतर श्रेढ़ी का सामान्य पद (13 – 2n) है, तो इसका सार्व अन्तर होगा :
(A) 0
(B) -13
(C) 2
(D) -2
Ans :- D
59. समांतर श्रेढ़ी 126, 120, 114……. का कौन-सा पद 0 है ?
(A) 20वाँ
(B) 21वाँ
(C) 22वाँ
(D) 23वाँ
Ans :- C
60. समांतर श्रेढ़ी 0, 1/8 , ¼ , 3/8 , …. का सार्व अंतर है :
(A) 1/8
(B) -1/8
(C) 1/4
(D) -1/4
Ans :- A
61. यदि समान्तर श्रेढ़ी का सामान्य पद (5n – 7) है, तो इसका प्रथम पद होगा :
(A) 0
(B) -7
(C) 2
(D) -2
Ans :- D
62. समांतर श्रेढ़ी 2, 6, 10, ……..के प्रथम 11 पदों का योगफल हैं:
(A) 240
(B) 242
(C) 248
(D) 200
Ans :- B
63. यदि किसी समांतर श्रेढ़ी का nवाँ पद 5 – 3n हो, तो इसका सार्व अंतर है :
(A) 5
(B) -3
(C) 4
(D) 3
Ans :- B
64. 21, 18, 15, ……. का कौन सा पद शून्य है ?
(A) 7वाँ
(B) 8वाँ
(C) 9वाँ
(D) 5वाँ
Ans :- B
65. समांतर श्रेढ़ी √7. √28, √63 ………का चौथा पद क्या है ?
(A) √70
(B) √84
(C) /98
(D) √112
Ans :- D
66. यदि 2/3 , a , 2 किसी समांतर श्रेढ़ी के तीन क्रमागत पद हैं तो a का मान होगा :
(A) 2/3
(B) 4/5
(C) 5/4
(D) 3/2
Ans :- B
67. यदि समांतर श्रेढ़ी का सार्व अंतर 3 है, तो a14 – a10 =
(A) 3
(B) 12
(C) 15
(D) 17
Ans :- B
68. समांतर श्रेढ़ी √3, √ 12, √27, √48 …… का सार्व अंतर है :
(A) √3
(B) -√3
(C) 2√3
(D) 2
Ans :- A
69. यदि समान्तर श्रेढ़ी का सामान्य पद (2n – 2) है, तो पहला पद है :
(A) 0
(B) 1
(C) 2
(D) -2
Ans :- A
70. निम्नलिखित में कौन समांतर श्रेढ़ी में है ?
(A) 2, 4, 8, 16, …
(B) 2, 22, 222, 2222,….
(C) -11, -7, -3, 1,…
(D) 3, 6, 12, 16, …….
Ans :- C
71. समांतर श्रेढ़ी 68, 63, 58, …….का 10वाँ पद है
(A) 12
(B) 15
(C) 18
(D) 23
Ans :- D
72. समांतर श्रेढ़ी 5, 9, 13, 17, …….का nवाँ पद होगा
(A) 5n – 1
(B) 6n – 1
(C) 4n – 1
(D) 4n + 1
Ans :- D
73. निम्नलिखित में कौन समांतर श्रेढ़ी में है ?
(A) 0.4, 0.44, 0.444,
(B) 1, 11, 111, …
(C) 2, 4, 8, 16, ….
(D) 0, -4, -8, -12 , …….
Ans :- D
74. समांतर श्रेढ़ी √18, √50, √98 , √162 का सार्व अंतर है :
(A) 2
(B) 2√2
(C) 3
(D) 2√3
Ans :- B
75. समांतर श्रेढ़ी 2, 5, 8, 11, …… का 11वाँ पद क्या होगा ?
(A) 24
(B) 30
(C) 32
(D) 14
Ans :- C
76. यदि किसी समांतर श्रेढ़ी का nवाँ पद 8n – 2 हो, तो उस श्रेढ़ी का सातवाँ पद होगा :
(A) 54
(B) 50
(C) 30
(D) 40
Ans :- A
77. यदि किसी समांतर श्रेढ़ी में a30 – a20 = 50 हो, तो श्रेढ़ी का सार्व अंतर होगा :
(A) 4
(B) 15
(C) 5
(D) 10
Ans :- C
78. समांतर श्रेढ़ी 2, 6, 10, 14, ……. 82 में पदों की संख्या है :
(A) 15
(B) 21
(C) 20
(D) 22
Ans :- B
79. एक समांतर श्रेढ़ी के प्रथम तीन पद क्रमश: (3y -1), (3y + 5) तथा (5y + 1) है, y का मान है :
(A) -3
(B) 4
(C) 5
(D) 2
Ans :- C
80. A.P.6,9,12, …… का सार्व अंतर है :
(A) 3
(B) -3
(C) 6
(D) -6
Ans :- A
81. 8, 5, 2, ……. का 40वाँ पद है
(A) – 107
(B) 109
(C) – 111
(D) – 113
Ans :- B
82. A.P. 11, 15, 19, ……. का कौन-सा पद 51 है ?
(A) 9वाँ
(B) 10वाँ
(C) 11वाँ
(D) 12वाँ
Ans :- C
83. किसी समान्तर श्रेढ़ी का दूसरा पद 13 और इसको 5वाँ पद 25 है। इसका सार्व अंतर होगा :
(A) 2
(B) 3
(C) 4
(D) 5
Ans :- C
84. यदि समांतर श्रेढ़ी का nवाँ पद 5 – 3n हो, तो इसका सार्व अंतर है :
(A) 3
(B) -3
(C) 4
(D) 5
Ans :- B